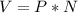
ответ: y=-4/25*e^(2*x)+5/25*x*e^(2*x)+4/25*cos(x)+3/25*sin(x).
Объяснение:
Перед нами - неоднородное ЛДУ 2-го порядка с правой частью специального вида f(x)=e^(m*x)*[P1(x)*cos(n*x)+P2(x)*sin(n*x)], где m=0, P1(x)=0, P2(x)=1, n=1. Его общее решение yо=y1+y2, где y1 - общее решение однородного уравнения y"-4*y'+4*y=0, а y2 - частное решение данного неоднородного уравнения.
1) Найдём y1. Характеристическое уравнение (ХУ) имеет вид k²-4*k+4=(k-2)²=0, его решениями являются k1=k2=2. Так как корни ХУ - действительные и равные, то y1 имеет вид: y1=C1*e^(2*x)+C2*x*e^(2*x).
2) Переходим к отысканию y2. Так как числа m+i*n и m-i*n, то есть +i и -i, где i=√(-1), не являются корнями ХУ, то y2 ищем в виде y2=e^(m*x)*[R1(x)*cos(n*x)+R2(x)*sin(n*x)], где R1(x) и R2(x) - многочлены, степень которых равна старшей из степеней многочленов P1(x) и P2(x). Так как эта старшая степень равна нулю, то положим R1(x)=a, R2(x)=b, где a и b - неизвестные пока постоянные числа. И так как при этом m=0 и n=1, то y2=a*cos(x)+b*sin(x). Дважды дифференцируя y2, находим y2'=-a*sin(x)+b*cos(x), y2"=-a*cos(x)-b*sin(x). Подставляя теперь y2, y2' и y2" в исходное уравнение и приводя подобные члены, приходим к уравнению 3*a*cos(x)+3*b*sin(x)+4*a*sin(x)-4*b*cos(x)=sin(x), или sin(x)*[4*a+3*b]+cos(x)*[3*a-4*b]=sin(x). Отсюда следует система уравнений относительно a и b:
4*a+3*b=1
3*a-4*b=0
Решая её, находим a=4/25, b=3/25. Отсюда y2=4/25*cos(x)+3/25*sin(x) и тогда yо=y1+y2=C1*e^(2*x)+C2*x*e^(2*x)+4/25*cos(x)+3/25*sin(x). Дифференцируя yо, находим yо'=2*C1*e^(2*x)+C2*e^(2*x)+2*C2*x*e^(2*x)-4/25*sin(x)+3/25*cos(x). Используя теперь условия yо(0)=0 и yо'(0)=0, приходим к системе уравнений:
C1+4/25=0
2*C1+C2+3/25=0
Решая её, находим C1=-4/25, С2=5/25. Тогда искомое частное решение уравнения yч таково: yч=-4/25*e^(2*x)+5/25*x*e^(2*x)+4/25*cos(x)+3/25*sin(x).