Рассмотрим последние цифры степеней чисел 3 и 7 (очевидно, степени чисел 33 и 77 оканчиваются на те же цифры; в таблице последняя цифра числа x обозначена как x mod 10):

Дальше таблицу можно не продолжать: поскольку последняя цифра степени определяется только последней цифрой предыдущей степени, то дальше всё будет повторяться: например, для степеней тройки дальше идут 3, 9, 7, 1, 3, 9, ... Таким образом, последовательность последних цифр степеней тройки и семёрки является периодической с периодом 4, то есть прибавление любого количества четвёрок к показателю степени последнюю цифру не меняет.
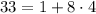 , поэтому
, поэтому 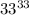 оканчивается на ту же цифру, что и
оканчивается на ту же цифру, что и  , то есть на 3.
, то есть на 3. 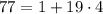 , поэтому
, поэтому  оканчивается на ту же цифру, что и
оканчивается на ту же цифру, что и  , то есть на 7. Значит, сумма
, то есть на 7. Значит, сумма  оканчивается на ту же цифру, что и
оканчивается на ту же цифру, что и 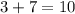 , то есть на 0. Искомый остаток равен нулю.
, то есть на 0. Искомый остаток равен нулю.
ответ. 0
1) S=-32+5*3/2 *6=-51 S=(3k-32)*(k+1)/2
2) S=4+11*2/2 *12=156 S=(2-2√3+11*(-√3))/2 *12=(2-13√3)*6=12-78√3
3)хn= 3n+2=a1+(n-1)d значит d=3 a1=5 значит S=(10+4*5)/2 *5=75 S=(10+39*5)/2 *40=4100
S=(10+(k-1)5)/2 *k
4)а1=5 d=5 чисел таких 100/5=20 S=(10+19*5)/2 *20=1050
a1=2 d=2 n=50 S=(4+49*2)/2 *50=2550
5)24=8+6d d=8/3 S=(16+8*8/3)/2 *9=168