ответ: (2,5;+∞).
Объяснение:
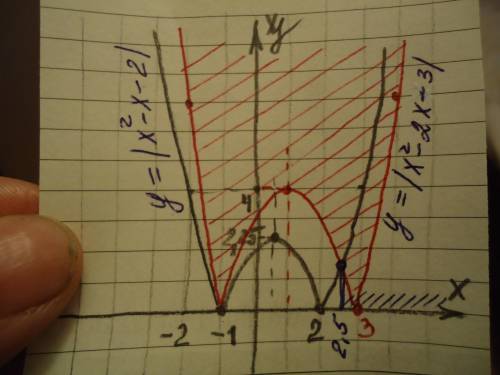
Можно построить графики функций у=|х²-х-2| и у=|х²-2х-3|.
См. рисунок на фото.
На рисунке заштрихованная зона соответствует тем значениям, при которых значения любой другой функции будут больше у=|х²-2х-3| и в эту зону попадает часть графика функции у=|х²-х-2| , начиная от их точки пересечения, не равной нулю.
Найдём координаты этой точки:
при х=2 х²-х-2=0, а при х>2 х²-х-2>0;
при х=3 х²-2х-3=0, а при х∈(2;3) х²-2х-3<0 ⇒
х²-х-2= -х²+2х+3;
2х²-3х-5=0;
D=9+4*2*5=9+40=49=7²;
х₁₂=(3±7):4;
х₁=2,5 и х₂= -1 -не подходит, т.к. при этом значении х обе функции равны нулю.
При х= 2,5 у=2,5²-2,5-2=6,25-4,5=2,25.
(2,5; 2,25) - искомая точка пересечения ⇒ при х∈(2,5;+∞) график первой функции больше второй.
ответ: (2,5;+∞).
Объяснение:
х дет./день - производительность первого рабочего
у дет./день - производительность второго рабочего
За три дня первый изготовил на 60 деталей больше, чем второй за два дня: 3х - 2у = 60
Вместе изготовили деталей: 15х + 14у = 1020
Получили систему уравнений:
3х - 2у = 60
15х + 14у = 1020
3х - 2у = 60
2у = 3х-60
у = (3х - 60) : 2
у = 1,5х - 30
15х + 14у = 1020
15х + 14*(1,5х - 30) = 1020
15х + 21х - 420 = 1020
36х = 1020 + 420
х = 1440 : 36
х = 40 (дет/день) - производительность первого рабочего
у = 1,5*40 - 30 = 60 - 30 = 30 (дет/день) - производительность второго рабочего
15*40 = 600 (деталей) - изготовил первый рабочий за 15 дней
14*30 = 420 (деталей) - изготовил второй рабочий за 14 дней