На стержень длиной 20 сантиметров и радиусом 1/(2\pi) сантиметров намотали нитку, начиная с одного края стержня и заканчивая на другом. оказалось, что было сделано ровно 15 оборотов. какой минимальной могла быть длина нитки (в сантиметрах)?

👇

Ответ:

pvltozq6wl

01.04.2022

Длина одного витка можно вычислить по теореме Пифагора

$L^2 = (L_{ok})^2+t^2 = ( 2\pi R)^2 + t^2$

где Lok - длина окружности;
R - радиус стержня;
t - шаг витка, который определяется

$t = \frac{L_{CT}}{n} = \frac{20}{15}$

где Lcт = 20 см - длина стержня
n = 15 число оборотов

Определим длину нитки

$L = n * \sqrt{( 2\pi R)^2 + t^2} = 15 * \sqrt{(2 \pi * \frac{1}{2 \pi } )^2 +( \frac{20}{15})^2} = \\ \\ = 15 * \frac{ \sqrt{15^2+20^2} }{15} = \sqrt{625} = 25$

ответ: 25 см
$На стержень длиной 20 сантиметров и радиусом 1/(2\pi) сантиметров намотали нитку, начиная с одного к$

4,8(32 оценок)

Открыть все ответы

Ответ:

агент007200

01.04.2022

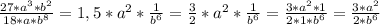
$\frac{27*a^3*b^2}{18*a*b^8}=1,5*a^2*\frac{1}{b^6}=\frac{3}{2}*a^2*\frac{1}{b^6}=\frac{3*a^2*1}{2*1*b^6}=\frac{3*a^2}{2*b^6}$

Объяснение:

Степень числа, это произведение множителей, каждый из которых величиной , 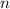раз подряд, где

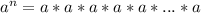
a^n=a*a*a*a*a*...*a

Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого числа вычитают показатель степени делителя:

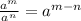
$\frac{a^m}{a^n}=a^{m-n$

Где 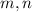m,n - любые натуральные числа, с условием, что .

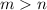Запишем наш пример:

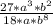
$\frac{27*a^3*b^2}{18*a*b^8}$

Для наглядности решения данный пример можно разделить на три части, и согласно свойству частного степеней, которое я записал выше можно было проще решить данный пример.

Первой частью будут известные числа:

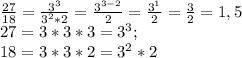$\frac{27}{18}=\frac{3^3}{3^2*2}=\frac{3^{3-2}}{2}=\frac{3^1}{2}=\frac{3}{2}=1,5\\27=3*3*3=3^3;\\18=3*3*2=3^2*2$ (1)

Теперь запишем отдельно деление переменной :

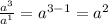$\frac{a^3}{a^1}=a^{3-1}=a^2$ (2)

Далее запишем переменную :

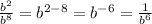$\frac{b^2}{b^8}=b^{2-8}=b^{-6}=\frac{1}{b^6}$ (3)

Так как по определению отрицательной степени: $b^{-n}=\frac{1}{b^n}$

Теперь совместим (1), (2) и (3):

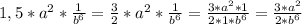$1,5*a^2*\frac{1}{b^6}=\frac{3}{2}*a^2*\frac{1}{b^6}=\frac{3*a^2*1}{2*1*b^6}=\frac{3*a^2}{2*b^6}$ - в дальнейшем данную дробь сократить невозможно, это и будет ответ.