Найти частное решение линейного неоднородного уравнения 2-го порядка.
Алгоритм решения неоднородного ДУ следующий:
1) Сначала нужно найти общее решение соответствующего однородного уравнения y``+y`-2y=0
Составим и решим характеристическое уравнение:
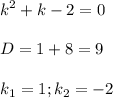
получены различные действительные корни, поэтому общее решение:
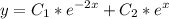
2) Теперь нужно найти какое-либо частное решение неоднородного уравнения
в правой части 4e²ˣ-2x+1. Значит предположу что частное решение неоднородного уравнения нужно искать в виде: y=Аe²ˣ+Bx+C
Найдём первую и вторую производную:
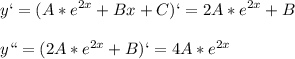
подставим в левую часть
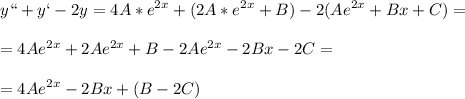
и теперь приравняем к правой
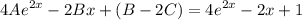
отсюда составим систему
![\displaystyle \left \{ {{4A=4; -2B=-2} \atop {B-2C=1}} \right. \]\\\\A=1; B=1;C=0](/tpl/images/3220/5151/2929a.png)
3) Запишем общее решение неоднородного уравнения:
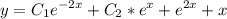
4) теперь найдем частное решение
y(0)=3; y`(0)=5
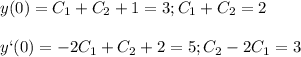
решая систему получим
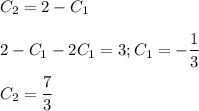
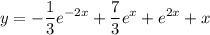
Дан равнобедренный треугольник с вершинами А (-4;-1) ,B (2; -9), C (7; 1) Найти длину его биссектрисы проведенной к основанию.
Расчет длин сторон
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √100 = 10.
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √125 = 11,18034.
AC (в) = √((Хc-Хa)²+(Ус-Уa)²) = √125 = 11,18034.
Как видим, стороны ВС и АС равны. Треугольник равнобедренный.
В равнобедренном треугольнике биссектриса СН к основанию (а это сторона АВ) является и высотой.
СН = √(125 - (10/2)²) = √(125 - 25) = √100 = 10.
ответ: биссектриса равна 10.
F'(x)=[(2-3x)/(x-1)]'+[x^4*√(2-x)]'+[3sin(пи/2-2x)]'
[(2-3x)/(x-1)]'=[u/v]'=1/v²[u'v-v'u] u=2-3x u'=-3 v=x-1 v'=1
[(2-3x)/(x-1)]'=1/x²[-3x²+3-2-3x]=-1/x²[3x²+3x-1]
[x^4*√(2-x)]'=u'v+v'u u=x⁴ u'=4x³ v=√(2-x) v'=1/2√(2-x)
[x^4*√(2-x)]'=4x³*√(2-x) + x⁴/2√(2-x)
[3sin(пи/2-2x)]'=3*(-2)cos(пи/2-2x)=-6sin2x
F'(x)=-1/x²[3x²+3x-1]+4x³*√(2-x) + x⁴/2√(2-x)-6sin2x