Объяснение:
P(x) = 2x⁴ + 11x³ - 3x² + 17x -13;
Q(x) = x + 6.
Замечание: Поскольку двучлен принято записывать в виде (x-a), то
Q(x) = x - (-6).
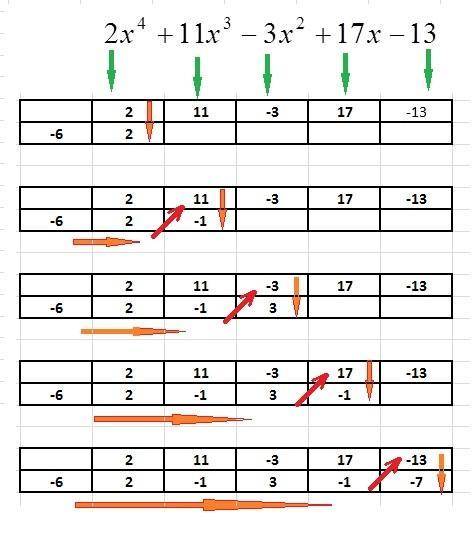
Применим табличный метод применения схемы Горнера.
В первую строчку таблицы переносим коэффициенты 2; 11; -3; 17; -13
Во второй строке слева записывем (-6).
Далее просто копируем коэффициент (2) из первой строки во вторую.
Действуем по алгоритму (смотри приложение):
(-6)*2 + 11 = -1
(-6)*(-1) + (-3) = 3
(-6)*3 + 17 = -1
(-6)*(-1) - 13 = -7
ответ.
Частное:
(2x³ - x² +3x -1)
Остаток:
(- 7) / (x+6)
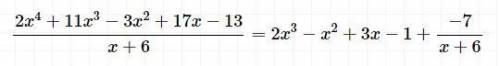
пусть числом при делении которого на 10 получается остаток 3 будет 33, а другое число 55. остаток от деления на 10 их суммы найдем следующим образом:
33+55=88
88 : 10 = 8 Остаток 8