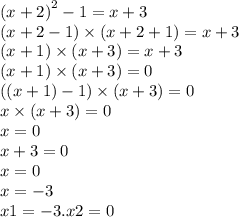
Такие распределения, как биномиальное, показательное, нормальное, являются семействами распределений, зависящими от одного или нескольких параметров. Например, показательное распределение с плотностью вероятностей , зависит от одного параметра λ, нормальное распределение- от двух параметровmи σ. Из условий исследуемой задачи, как правило, ясно, о каком семействе распределений идёт речь. Однако остаются неизвестными конкретные значения параметров этого распределения, входящие в выражения интересующих нас характеристик распределения. Поэтому необходимо знать хотя бы приближённое значение этих величин.
Пусть закон распределения генеральной совокупности определён с точностью до значений входящих в его распределение параметров , часть из которых может быть известна. Одной из задач математической статистики является нахождение оценок неизвестных параметров по выборке наблюденийиз генеральной совокупности. Оценка неизвестных параметров заключается в построении функцииот случайной выборки, такой, что значение этой функции приближённо равно оцениваемому неизвестному параметруθ. θ.
Статистическойоценкой(в дальнейшем простооценкой) параметраθтеоретического распределения называется его приближённое значение, зависящего от данных выбора.
Оценка является случайной величиной, т.к. является функцией независимых случайных величин ; если произвести другую выборку, то функция примет, вообще говоря, другое значение.
Существует два вида оценок – точечные и интервальные.
Точечнойназывается оценка, определяемая одним числом. При малом числе наблюдений эти оценки могут приводить к грубым ошибкам. Чтобы избежать их, используют интервальные оценки.
Интервальнойназывается оценка, которая определяется двумя числами – концами интервала, в котором с заданной вероятностью заключена оцениваемая величинаθ.
ЗАДАЧА:
Расстояние от точки А до точки В= 62 км. На расстоянии 30 км от точки А находится точка С. Из точки А в точку С выехал велосипедист со скоростью 12км/ч, а через 30 минут из точки В в точку С выехал мотоциклист.
ВОПРОС 1: с какой скоростью должен ехать мотоциклист, чтобы встретиться с велосипедистом в точке С?
ВОПРОС 2:
С какой скоростью должен ехать мотоциклист, чтобы приехать в точку С раньше велосипедиста на 1 час 10 минут?
Объяснение:
если от точки А до точки С 30км, то от точки
С до В=62–30=32км. Поэтому велосипедисту до точки С нужно проехать 30км, а мотоциклисту из точки В до точки С - 32 км
Велосипедист со скоростью 12км/ч проедет расстояние 30км за: 30÷12=5/2=2,5 часа
1 ч 10 мин=1 целая 1/6часа или 7/6часа.
Чтобы мотоциклист доехал до точки С раньше велосипедиста на 7/6часа, тогда:
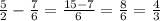
Итак: мотоциклисту нужно добраться до точки С за 4/3 часа. Для этого ему понадобится:
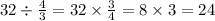
ОТВЕТ 2: мотоциклисту нужно ехать со скоростью 24км/ч, чтобы приехать раньше велосипедиста на 1 час 10 минут.
РЕШЕНИЕ Вопроса 1
30минут=1/2=0,5 часа
Так как мотоциклист выехал через 30 минут после
велосипедиста, то велосипедист за 30 минут проехал: 12÷2=6км и ему осталось проехать 30–6=24км и ему понадобится на это:
2,5 –0,5=2часа.
Соответственно мотоциклисту до встречи с велосипедистом в точке С понадобится также 2часа.
Мотоциклисту нужно за 2 часа проехать 32 км, поэтому ему нужно ехать со скоростью: 32÷2=16км/ч
ОТВЕТ 1: чтобы встретиться с велосипедистом в точке С мотоциклисту нужно ехать со скоростью 16км/ч