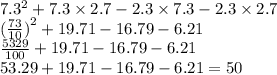
Два рабочих могут выполнить заказ за 12 дней.Если половину работы выполнит первый рабочий,а затем его сменит второй рабочий,то весь заказ будет выполнен за 25 дней.За сколько дней каждый рабочий в отдельности выполнит данный заказ!
Решение
За х дней первый рабочий в отдельности выполнит данный заказ
за у дней второй рабочий в отдельности выполнит данный заказ
Пусть 1 - объём всего заказа (т.е. вся работа), тогда
1/х - часть работы, которую выполняет первый рабочий за 1 день (т.е. производительность первого)
1/у - производительность второго рабочего за 1 день
Первое уравнение получаем через общую производительность:
1/х + 1/у = 1/12
Упростив, получим:
12(х+у) = ху
Для второго уравнения найдем время, за которое выполнит половину всего заказа 1/2 каждый рабочий, работая в отдельности:
1/2 : 1/х = х/2 дней - это время за которое половину работы выполнит первый рабочий
1/2 : 1/у = у/2 дней - это время за которое половину работы выполнит второй рабочий
Получаем второе уравнение:
х/2 + у/2 = 25
Упростив, получим:
х + у = 50
Решаем систему:
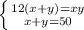
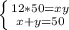
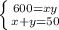
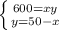
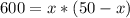
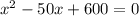
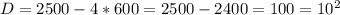
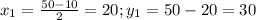
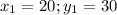
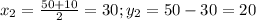
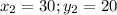
ответ: 20; 30
sin(x²+x)=1/2
x²+x = (-1)ⁿarcsin(1/2) + πn, n∈Z;
x²+x = (-1)ⁿπ/6 + πn, n∈Z;
x² + x - (-1)ⁿπ/6 - πn = 0;
D = 1 + 4·((-1)ⁿπ/6 - πn);
D₁ = 1 + 4·(π/6 - 2πn); D₁ ≥ 0; 1 + 4·(π/6 - 2πn) ≥ 0; π/6 - 2πn ≥ -0,25| · 6;
π - 12πn ≥ -1,5; 12πn ≤ π + 1,5; n ≤ (π + 1,5)/(12π); n ≤ (2π + 3)/(24π);
n ≤ 1/12 + 3/(8π); n = 0; -1; -2;
x₁ = (-1 + √(1 + 4·(π/6 - 2πn)))/2; x₂ = (-1 - √(1 + 4·(π/6 - 2πn)))/2, n = 0; -1; -2;
D₂ = 1 + 4·(-π/6 - 2πn - π) = 1 + 4·(-7π/6 - 2πn) ; D₂ ≥ 0; 1 + 4·(-7π/6 - 2πn) ≥ 0;
-7π/6 - 2πn ≥ -1/4; 2πn ≤ 1/4 - 7π/6; n ≤ (1/4 - 7π/6)/(2π);
n ≤ 1/(8π) - 7/12; n = -1; -2; -3; ...
x₁ = (-1 + √(1 + 4·(-7π/6 - 2πn)))/2; x₂ = (-1 - √(1 + 4·(-7π/6 - 2πn)))/2, n = -1; -2; -3; ...