Участник roperd решил данное неравенство методом интервалов, однако этот метод - далеко не единственный метод решения подобных неравенств. Я считаю, что вам будет полезно о них знать.
Во-первых, левую часть данного неравенства можно преобразовать в квадратный трёхчлен, раскрыв скобки:
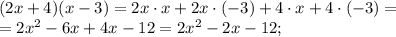
Т.е., перед нами квадратное неравенство, которое можно решить функциональным Для этого необходимо рассмотреть квадратичную функцию 
, и найти на оси x, используя график, такие значения аргумента, при которых значение данной функции будет больше или равно нулю:
1) y=0, ес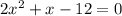ли 
или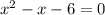 
; найдём корни этого уравнения, например, через дискриминант:
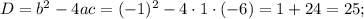
Дискриминант положительный, значит данное уравнение имеет два корня:
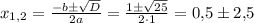
т.е., это -2 и 3.
Это значит, что парабола пересеает ось x в точках с абсциссами -2 и 3. И, так как парабола имеет направленные вверх ветви(старший коэффициент положителен), то отрицательные значения y будут находиться ниже этой оси, т.е.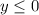 
, ес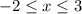ли 
или ![x \in [-2;\ 3]](/tpl/images/0065/5427/536c0.png)
, что, кстати говоря, не соответствует не одному из приведённых вариантов ответа, вероятно, вы допустили ошибку, вводя их.
Можно также использовать правило расщепления, когда неравенство определённого вида представляют, как совокупность равноцсильных систем неравенств, попробуйте что-либо узнать о нём.
б) (√10+4)(4-√10) = (4 + √10)(4 - √10) = 16 - 10 = 6