6543 и 6210
Объяснение:
Рассматриваются четырёхзначные числа M, среди которых нужно выбрать числа, удовлетворяющие условиям:
1) 6000 < M < 7000;
2) M делится на 9;
3) каждая следующая цифра M меньше предыдущей.
Если представить число M в виде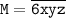 
, где хотя-бы один из цифр x или y или z отличен от 0, то 1-условие выполнено. Но, если выполняется 3-условие, то есть если 6>x>y>z, то 1-условие выполняется.
Рассмотрим все числа вида 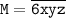, для которых выполнено 3-условие:
6543, 6542, 6541, 6540, 6532, 6531, 6530, 6521, 6520, 6510;
6432, 6431, 6430, 6421, 6420, 6410;
6321, 6320, 6310;
6210.
Остается проверить 2-условие для этих чисел. Используем признак делимости на 9:
Число А делится на 9 ⇔ Сумма цифр числа А делится на 9.
Нетрудно проверить, что только следующие числа делятся на 9:
6543 (6+5+4+3=18) и 6210 (6+2+1+0=9).
1.
6x²y - 2z²y + xy² - 7xy² = 6x²y - 2z²y - 6xy²
Привели подобные и получили многочлен стандартного вида:
6x²y - 2z²y - 6xy²
Определим степень каждого одночлена:
1) 6x²y = 6х²у¹ (складываем показатели степеней 2+1=3)
2)2z²y = 2z²y¹ (складываем показатели степеней 2+1=3)
3) 6xy² = 6х¹у² (складываем показатели степеней 1+2=3)
Каждый его одночлен имеет степень равную 3, поэтому в ответе указывается степень многочлена 3.
2.
a² + 5a - 3 + 2a² - 4a + 9 = 3а² - а + 6
Получили многочлен стандартного вида:
3а² - а + 6
Определим степень каждого одночлена:
1) 3а² (степень 2)
2) - а (степень 1)
3) 6 (степень 0)
Степенью многочлена стандартного вида называют наибольшую из степеней, входящих в его запись.
Наибольшая равна 2.
ответ: 2
(-5-3=-8; 2-2=0; 3+5=8) = (-8; 0; 8).