




 и
и 
1)
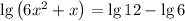
При решении логарифмических уравнений всегда сначала нужно находить область определения. Аргумент логарифма всегда должен быть положительным, а основание - не только положительным, но и неравным единице. С основаниями всё в порядке, поскольку 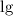 - это логарифм с основанием 10. Теперь с аргументами. 12 и 6 положительны, а вот у логарифма в левой части уравнения в аргументе находится переменная, а потому область определения является решением неравенства:
- это логарифм с основанием 10. Теперь с аргументами. 12 и 6 положительны, а вот у логарифма в левой части уравнения в аргументе находится переменная, а потому область определения является решением неравенства:
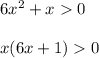
Нули: 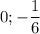 .
.
+ - +
--------------------о---------------------------о-----------------------> x
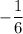
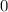
Таким образом, запишем область определения функции:
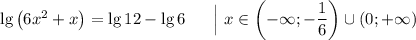
По свойству логарифма: 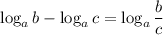 , тогда для нашего случая:
, тогда для нашего случая:
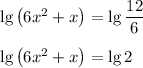
Так как основания логарифмов одинаковые, мы можем приравнять аргументы.
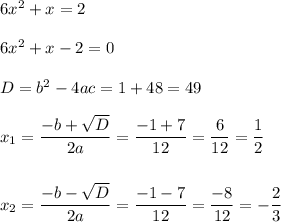
Оба корня входят в выведенную нами область определения, а потому они оба являются решениями уравнения.
ответ: 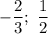 .
.
2)
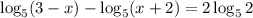
Для нахождения области определения проверяем каждое расписанное мной сверху свойство для каждого логарифма. В итоге должно получиться:
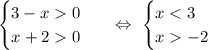
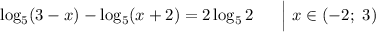
Теперь воспользуемся двумя свойствами логарифмов. Первое мы применяли в уравнении, а второе: 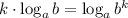 .
.
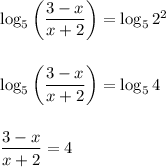
По основному свойству пропорции:
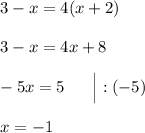
Корень входит в область определения, а значит, является решением уравнения.
ответ: -1.
3)
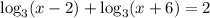
Уже по стандарту находим область определения.
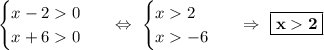
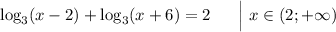
Воспользуемся свойством логарифма: 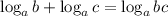 . Двойку в правой части нам нужно заменить на тождественный ей логарифм по основанию 3, таким будет
. Двойку в правой части нам нужно заменить на тождественный ей логарифм по основанию 3, таким будет 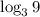 .
.
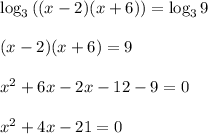
По теореме Виета:

А теперь внимание, то, зачем мы искали область определения. Напомню, она у нас была 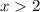 . Найденный нами корень -7 в этот промежуток не входит, а потому решением уравнения НЕ ЯВЛЯЕТСЯ. С корнем 3 же всё нормально, а значит, уравнение имеет одно решение.
. Найденный нами корень -7 в этот промежуток не входит, а потому решением уравнения НЕ ЯВЛЯЕТСЯ. С корнем 3 же всё нормально, а значит, уравнение имеет одно решение.
ответ: 3.
4)
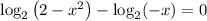
Область определения:
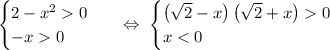
Верхнее неравенство решим отдельно.
Нули: 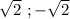 .
.
- + -
-----------------------о---------------------------о-----------------------> x
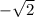
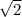
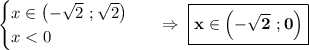
0 - это логарифм с аргументом 1, при этом основание может быть любым допустимым. Например, 2, как в нашем случае: 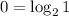 . Пользуемся тем же свойством.
. Пользуемся тем же свойством.
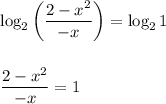
Откуда получаем, что:
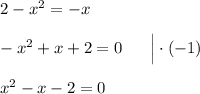
По теореме Виета:

Опять сравниваем с областью определения. Легко заметить, что 2 в неё не входит, а значит, НЕ ЯВЛЯЕТСЯ РЕШЕНИЕМ. А -1 входит туда, поэтому уравнение имеет одно решение.
ответ: -1.
1. Задание на грамматику. Употребите глаголы в скобках в Present Simple.
1. She (go) ……… to school every day.
2. I (skate) ……… every winter.
3. We (do) ……… our homework on Mondays.
4. My mum (make) ……… cakes every Sunday.
2. Задание на грамматику. Употребите в предложении модальный глагол must или must not.
1. You ……… swim here, because it is very dangerous.
2. Children ……… help their parents.
3. A boy has got a pet, so he ……… take care of it.
4. These boys are hooligans. You ……… play with them.
5. He ……… go out. It is very cold.
3. Задание на грамматику. Выберите местоимение many или much.
1) I don’t like ……… sugar in my tea.
2) There isn’t ……… milk in the fridge.
3) There are so ……… stars in the sky.
4) Are there ……… children on the beach?
5) How ……… money have we got with us?
Объяснение: