Объяснение:Скорость парохода в стоячей воде обозначим v км/ч. Скорость течения нам известна - 4 км/ч. По течению пароход км со скоростью v + 4 км/ч, против течения еще 48 км со скоростью v - 4 км/ч, и затратил на все это 5 ч времени. Составляем уравнение: 48/(v + 4) + 48/(v - 4) = 5 переносим 5 влево и приводим к общему знаменателю: [ 48*(v - 4) + 48*(v + 4) - 5(v + 4)(v - 4) ] / [ (v + 4)(v - 4) ] = 0 Числитель приравниваем к 0 и раскрываем скобки: 48v - 4*48 + 48v + 4*48 - 5(v^2 - 16) = 0 Раскрываем скобки и приводим подобные: 96v - 5v^2 + 80 = 0 Меняем знак: 5v^2 - 96v - 80 = 0 D/4 = 48^2 + 5*80 = 2304 + 400 = 2704 = 52^2 v1 = (48 - 52) / 5 < 0 v2 = (48 + 52) / 5 = 20 ответ: 20 км/ч.
Пусть х (км/ч) - скорость катера, тогда скорость катера по течению равна х+3 (км/ч), а против течения - х-3 (км/ч). Известно, что по течению катер проплыл 5 часов, в то время как против течения - 7 часов. Найдем пройденный путь для каждой ситуации:
S1 = (x+3)t1 - путь пройденный по течению, где t1 = 5ч
S2 = (x-3)t2 - путь пройденный против течения, где t2=7ч
Так как в обоих случаях пройден один и тот же путь, то S1 = S2. Приравняем их формулы и получим:
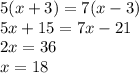
Таким образом, скорость катера в стоячей воде равна 18 км/ч.
По течению катер проплыл:
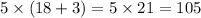
км
9-х²≥0 х²-9≤0 (х-3)(х+3)≤0 -3≤х≤3
х^2-х-2≠0 х≠4 х≠2 х≠2