1) Аналитический.
2) Рекуррентній.
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)
6)
7) Это арифметическая прогрессия.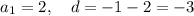 
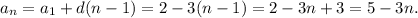
8)
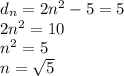
ответ: нет, не является, потому что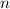 
должно быть натуральным числом.
9) 
Наибольшее натуральное 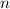, удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
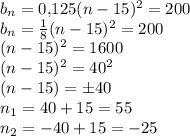
Второе решение не подходит, поскольку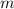 
должно быть натуральным числом.
ответ: 
1) Аналитический.
2) Рекуррентній.
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)
6)
7) Это арифметическая прогрессия.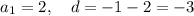
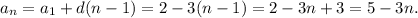
8)
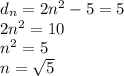
ответ: нет, не является, потому что 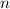должно быть натуральным числом.
9)
Наибольшее натуральное 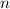, удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
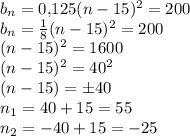
Второе решение не подходит, поскольку 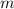должно быть натуральным числом.
ответ:
А(2;4) , В(2;7)
Так как точки А и В имеют одинаковые значения х=2, то они лежат на прямой х=2.
Расстояние от точки А до точки В равно 7-4=3 ⇒ сторона квадрата а=3.
Координаты других вершин квадрата: D₁(2+3;4)=D₁(5;4) и C₁(2+5;7)=C₁(7;7) , либо D₂(2-3;4) =D₂(-1;4) и C₂(2-3;7)=C₂(-1;7) .
Ещё один квадрат можно построить, если точки А и В принять за концы диагонали квадрата. Тогда точки C и В имеют координаты: С(0,5 ; 5,5) и D(3,5 ; 5,5) .