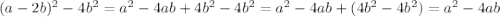Нули функции - это значения аргументы, при котором функция равна нулю : a) y= (x-1)/x² (x-1)/x² = 0 ОДЗ : x² ≠ 0 x ≠ 0 x - 1 = 0 x = 1 Нуль функции, это 1. Т.е., при x=1, y = 0 ответ : x=1
2) y=(x²+1)/(x-1) (x²+1)/(x-1)=0 ОДЗ : x-1 ≠ 0 x ≠ 1 x²+1 = 0 x² ≠ -1 x² не может быть равен отрицательному числу, т.к. число в квадрате всегда будет положительным, значит : x ∈ ∅ Функция нулей не имеет.
3) y=(3x-1)(x+7) (3x-1)(x+7) = 0 3x - 1 =0 и x + 7 = 0 3x = 1 | : 3 x = -7 x = 1/3 Нули функции x1 = 1/3, x2 = -7 Т.е., при x=1/3 и x=-7, y будет равен 0 ответ : x1 = 1/3, x2 = -7
Ясно, что двигаясь вниз и вправо, независимо от формы пути, Фоксу нужно будет сделать 6 ходов, чтобы из левой верхней клетки попасть в правую нижнюю. Из этих шести ходов 3 обязательно будут ходами на одну клетку вниз, а 3 - ходами на одну клетку вправо. Поскольку после каждого ходачисло под фишкой меняется, то имеем перестановку из 6 элементов двух разных типов, по три каждого типа. Чтобы подсчитать общее количество вариантов достижения правой нижней клетки применяем формулу для числа перестановок n элементов с повторениями: P = n! / (n1! n2!), где n=6; n1=3 и n2=3. Подставляя, получаем P=6! / (3! 3!)=720/36=20 ответ:20
а)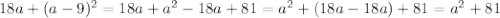
б)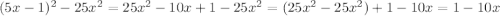
в)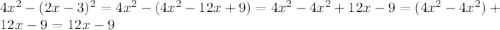
г)