Т.к. площадь (S) прямоугольного треугольника равна 42см^2, то
ab/2=S
где a и b катеты этого треугольника.
Т.к. сумма катетов равна 15,5 см, то
a+b=15,5
Составляем систему уравнений:
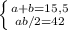
Выражаем из первого уравнения a:
a=15,5-b
Выражаем из второго уравнения a:
a=84/b
Подставляем и получаем:
15,5-b=84/b
Умножаем обе части уравнения на b и переносим все части этого уравнения в ghfde. часть:
b^2-15,5b+84=0
Находим дискрименант:
D=15,5^2-4*1*84=240,25-336<0
Дискрименант оказался отрицательным числом, следовательно уравнение нерешаемо, следовательно я доказал, что треугольник с такими соотношениями не существует!
P.S. 2 раза перепроверял.
Из исходного равенства видно, что p>q, в противном случае равенство не выполнялось бы. Предположим, что p=q+k, где k - натуральное. Тогда 2q+k=(q+k-q)^3, отсюда 2q+k=k^3 или 2q=k^3-k=k(k^2-1). Тогда q=k(k^2-1)/2. Отсюда сразу видно, что q будет простым только при k=2, поскольку при k=1 получаем 0, а при k>2 будем получать составные числа, а по условию q простое. Итак, при k=2, q=2*(2^2-1)/2=3. Тогда p=q+k=3+2=5. Это единственное решение удовлетворяющее данному равенству.
ответ: p=5, q=3.