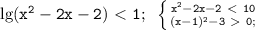
![\mathtt{\left\{{{x^2-2x+1-13\ \textless \ 0}\atop{(x-1)^2-(\sqrt{3})^2\ \textgreater \ 0}}\right\left\{{{(x-1)^2-(\sqrt{13})^2\ \textless \ 0}\atop{(x-1)^2-(\sqrt{3})^2\ \textgreater \ 0}}\right\left\{{{(x-[1-\sqrt{13}])(x-[1+\sqrt{13}])\ \textless \ 0}\atop{(x-[1-\sqrt{3}])(x-[1+\sqrt{3}])\ \textgreater \ 0}}\right}](/tpl/images/0849/1132/48f4e.png)
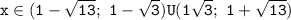
y = x³ - 4x²
Найдём производную :
y' = (x³)' - 4(x²)' = 3x² - 8x
Найдём критические точки, для этого приравняем производную к нулю.
y' = 0
3x² - 8x = 0
x(3x - 8) = 0
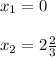
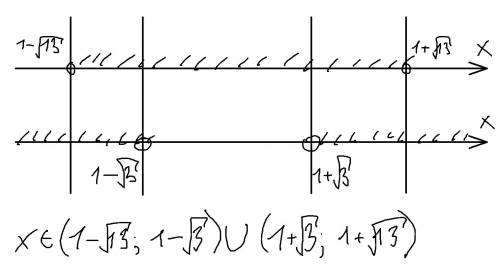
Отметим критические точки на числовой прямой и выясним знаки производной на промежутках, на которые эти точки разбивают числовую прямую .
y'(x) + - +
____________0___________2 2/3_____________
y(x) ↑ ↓ ↑
На промежутках (- ∞ ; 0] и [2 2/3 ; + ∞) -функция возрастает
На промежутке [0 ; 2 2/3] - функция уюывает
lg(x^2-2x-2)<lg10
x^2-2x-2<10
x^2-2x-12<0
D=4-4*(-12)=52
x=2+ 2 корня из 13/2=1+ корень из 13
х= 1- корень из 13
по методу интервалов : х = (1-корень из 13; 1+ корень из 13)
ОДЗ: x^2-2x-2>0
D=4-4*(-2)=12
x=2+2 корня из 3/2=1+ корень из 3
х=1-корень из 3
По методу интервалов: х=(-бесконечность, 1-корень из 3) объединенно с (1+корень из 3, +бесконечность)
ответ: (1- корень из 13;1- корень из 3) объединенно с (1+корень из 3, 1+корень из 13)