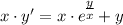
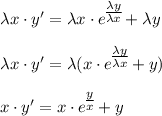
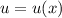 с замены:
с замены: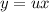 , тогда
, тогда 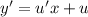
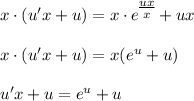
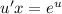
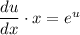 - уравнение с разделяющимися переменными.
- уравнение с разделяющимися переменными.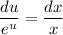 - уравнение с разделёнными переменными.
- уравнение с разделёнными переменными.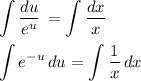
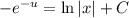 - общий интеграл новой функции.
- общий интеграл новой функции. из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену:
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: 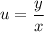
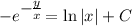 - общий интеграл исходного уравнения.
- общий интеграл исходного уравнения.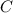 . Подставим в общий интеграл начальное условие:
. Подставим в общий интеграл начальное условие: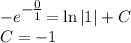
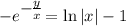 - частный интеграл, также является решением данного дифференциального уравнения.
- частный интеграл, также является решением данного дифференциального уравнения.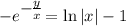
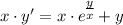
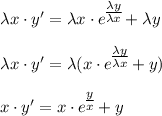
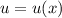 с замены:
с замены: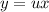 , тогда
, тогда 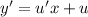
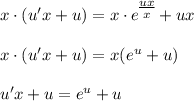
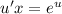
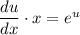 - уравнение с разделяющимися переменными.
- уравнение с разделяющимися переменными.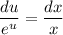 - уравнение с разделёнными переменными.
- уравнение с разделёнными переменными.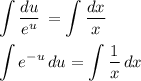
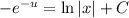 - общий интеграл новой функции.
- общий интеграл новой функции. из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену:
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: 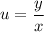
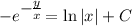 - общий интеграл исходного уравнения.
- общий интеграл исходного уравнения.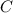 . Подставим в общий интеграл начальное условие:
. Подставим в общий интеграл начальное условие: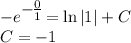
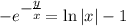 - частный интеграл, также является решением данного дифференциального уравнения.
- частный интеграл, также является решением данного дифференциального уравнения.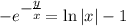
1 + x^2 + x^4 + ... при модуле х меньше 1 - это сумма членов бесконечно убывающей геометрической прогрессии, она равна
S = 1/(1 - x)
x + x^2(1 + x^2 + x^4 + ...)(1 - x) = x + x^2(1/(1-x))(1 - x) = x + x^2
Итак, строим график x^2 + х.