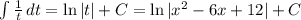
abx0>
Объяснение:
1) x-a >0 и x-b >0. Значит, x>a и x>b, т.е. a<x и b<x.
2) a²x < 0 . Значит, x<0, т.к. а²≥0. Но, по условию, х>a, значит а<0
3) Получаем, что a<0 и a<x, b<x
Т.е. точки a и b имеют отрицательные координаты и лежат левее точки Х на координатной прямой. Таким образом, возможно два случая, когда точка а расположена левее точки b или когда точка b расположена левее точки a.
abx0>
bax0>
В ответе изобразим одну из этих прямых.
Объяснение:
y=2x³ – 3x² +5 ; D(y) = R ;
a) y' = (2x³ – 3x² +5)' = 6x² - 6x = 6x( x - 1) ;
y' = 0; 6x( x - 1) = 0 ; x₁ = 0 ; x₂ = 1 ;
y'( - 1 ) > 0 ; y' (0,5) < 0 ; y'( 2 ) > 0 ; 77688yugyghvtftuyuyu
проміжки зростання ( - ∞ ; 0 ] i [1 ; + ∞ ) ;
проміжок спадання [ 0 ; 1 ] .
б) Точки 0 і 1 - екстремуми функції : х = 0 - точка максимуму функції ;
х = 1 - точка мінімуму функції .
в ) y=2x³ – 3x² +5 ; хЄ[ - 1 ; 2 ] ;
Точки 0 і 1 - екстремуми функції належать даному відрізку :
у( 0 ) = 2*0³ - 3*0² + 5 = 5 ;
у( 1 ) = 2*1³ - 3*1² + 5 = 4;
у( - 1 ) = 2*( - 1 )³ - 3*( - 1 )² + 5 = 0 ;
у( 2 ) = 2*2³ - 3*2² + 5 = 9 ;
max y( x ) = 9 ; min y( x ) = 0 на відрізку [- 1 ; 2 ] .