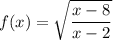
Подкоренное выражение должно быть неотрицательным, а знаменатель не равен нулю. При записи первого условия, второе учитывается. Тогда имеем:
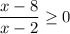
Решим методом интервалов:
Отмечаем на координатной прямой точки, в которых выражения из знаменателя и числителя обращаются в ноль. И выкалываем 2 т.к. на ноль делить нельзя. Мы получили 3 интервала. Перед дробью знак положителен, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (нету чётных степеней, где знак может не измениться). Нас интересует, когда больше или равно, поэтому выбираем интервалы с плюсом, учитывая их границы.
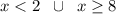
ответ: x∈(-∞;2)∪[8;+∞).

) 70-50=20 км/ч - скорость сближения.
2) 45/20=2 1/4 часа до встречи
3) 50*2 1/4=50*9/4=25*9/2=225/2=112,5 км от 2-го города - место встречи.
из двух городоы расположенных на одном шоссе
ответ на 157,5 км они встретятся и через 2 часа 15 мин
Это от первого города, два города на шоссе, которое идет неизвестно откуда, т. отсчета не указана. 2 1/4 ч и есть 2ч 15 мин. Одно и тоже. Вот 100км Горьковского - шоссе - это понятно: 100км от Горькова
Горький сейчас Нижний Новгород. Но шоссе Горьковское. Как Ленинград Санкт-Петербург, а область Ленинградская и вокзал Ленинградский
В силу того, что наименьший ПОЛОЖИТЕЛЬНЫЙ период косинуса
равен 2П, в конце формулы записывают слагаемое 2Пk (k∈Z). Но можно придавать значения переменной k не только положительные целые, а и отрицательные. Поэтому вторая группа корней может выглядеть так: