Пояснение:
Это квадратное уравнение можно решить сразу тремя : через теорему Виета и через Дискриминант (полный и краткий). Покажу все три.
(теорема Виета)
- можно применять, если первый (старший) коэффициент (а) равен единице (1), то есть квадратное уравнение имеет вид:
x² ± px ± q = 0.
x² + 8x + 15 = 0
p = 8; q = 15.
По т. Виета:
x₁ + x₂ = - 8,
x₁ × x₂ = 15.
x₁ = - 5,
x₂ = - 3.
<><><><><><><><><><><><><><><><>
IIа (Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
ax² ± bx ± c = 0.
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
D = b² - 4ac = 8² - 4 × 1 × 15 = 64 - 60 = 4 = 2².
D > 0 (значит, уравнение имеет два действ. корня)
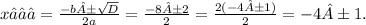
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
IIб ("краткий" Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
- можно применять к любым полным квадратным уравнениям вида:ax² ± bx ± c = 0,
где b - чётное число (то есть делится на 2 без остатка).
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
k = b ÷ 2 = 8 ÷ 2 = 4.
D₁ = k² - ac = 4² - 1 × 15 = 16 - 15 = 1.
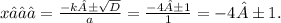
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
ответ: - 5; - 3.
Удачи Вам! :)
Найдём общее решение.
Выразим х.
5х = 11-3у
х = (11-3у)/5
Для того, чтобы х получился целым числом, нужно, чтобы числитель 11-3у был кратен 5. Это возможно, если он равен числу, заканчивающемуся на 0 или 5, т.е. 11-3у = m0 или 11-3у = m5, где m - старшие разряды. Тогда 3у =11- m0 = k1 или 3y =11- m5 = k6, где k - старшие разряды.
Для нахождения наименьшего целого числа, удовлетворяющего полученным условиям, нужно оставить только младший разряд, то есть разряд единиц.
3у = 1 3у = 6
у =1/ 3 у = 2
Итак, наименьшим целым числом, удовлетворяющем условию, будет 2. Следующее число, кратное 5, будет на 5 больше найденного, т.е. 2+5=7, следующее - ещё на 5 больше и т.д.
Следовательно, для у можно записать
у = 2+5·n, где n =0; 1; 2; ...; ∞
Отсюда найдём х:
х = (11-3·(2+5·n))/5 = (11-6-15·n)/5 = (5-15·n)/5 = 5·(1-3·n)/5 = 1-3·n, где n =0; 1; 2; ...; ∞
Но целые числа бывают также отрицательными. Найдём решение для отрицательных чисел.
5х = 11+3·(-у)
x = (11+3·(-у))/5
Для того, чтобы х получился целым числом, нужно, чтобы числитель 11+3·(-у) был кратен 5. Это возможно, если он равен числу, заканчивающемуся на 0 или 5, т.е. 11+3·(-у) = m0 или 11+3·(-у) = m5, где m - старшие разряды. Тогда 3·(-у) = m0-11 = k9 или 3·(-у) = m5-11 = k4, где k - старшие разряды.
Для нахождения наименьшего целого числа, удовлетворяющего полученным условиям, нужно оставить только младший разряд, то есть разряд единиц.
3·(-у) = 9 3·(-у) = 4
-y = 3 -y = 4/3
Итак, наименьшим целым числом, удовлетворяющем условию, будет 3. Следующее число, кратное 5, будет на 5 больше найденного, т.е. 3+5=8, следующее - ещё на 5 больше и т.д.
Следовательно, для у можно записать
-y = 3+5·n
y =-(3+5·n), где n = 0; 1; 2; ...; ∞
Отсюда найдём х:
х = (11+3·(3+5·n))/5 = (11+9+15·n)/5 = (20+15·n)/5 = 5·(4+3·n)/5 = 4+3·n
Итоговый ответ:
Для диапазона отрицательных чисел:
y =-(3+5·n),
где n = 0; 1; 2; ...; ∞
х =4+3·n,
Для диапазона положительных чисел:
у = 2+5·n,
где n =0; 1; 2; ...; ∞
х = 1-3·n
1 час 45 минут=105 минут
1 час 15 минут=75 минут
2 часа 55 минут=175 минут
a,b,c,d - производительности 1,2,3,4 трубы
Составляем уравнения:
a+b+c=1/105
a+b+d=1/75
c+d=1/175
Будем решать систему уравнений метод сложения.То есть, складываем все левые части и приравниваем их к сумме вторых частей уравнений:
a+b+c+a+b+d+c+d=1/175+1/75+1/105
2a+2b+2c+2d=1/105+1/75+1/175
2(a+b+c+d)=1/35
a+b+c+d=1/35:2=70
Значит, если включить все 4 трубы, то бассейн заполнится за 70 минут или 1 час и 10 минут.
Такие задачи надо решать с производительности.Не в коем случае не надо складывать просто время, за которое заполнит каждая труба.Это будет ошибкой!Удачи!