Объяснение:
Эта задача имеет два принципиально разных решения.
А) считаем, что все голубые шары одинаковы между собой, и все розовые тоже одинаковы.
Тогда:
1) двумя : вынуть розовый шар или вынуть голубой шар.
2) тоже двумя : сначала вынуть розовый шар, потом голубой, или наоборот, сначала голубой шар, а потом розовый.
Б) считаем, что все шары разные, например, имеют номера, как в бильярде.
Тогда:
.
Допустим, мы первым вынимаем голубой шар. Это 6 разных .
За ним вынимаем розовый, это 8 разных .
Всего вынуть сначала голубой шар, потом розовый.
И ещё вынуть, наоборот, сначала розовый шар, потом голубой.
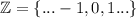
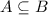 и
и 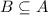
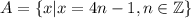
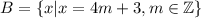


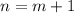
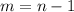
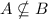 то,значит, есть такой элемент
то,значит, есть такой элемент 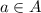 так что
так что 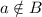 .
.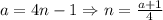
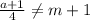
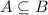
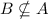 , то значит есть такой элемент
, то значит есть такой элемент 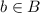 так что:
так что: 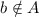
2)
3)
x/2+x/8=17/4
4x + x = 34
5x = 34
x = 34 : 5
x = 6,8
4)
x+1/4+x/3=2
12x + 3 + 4x = 2·12
16x + 3 = 24
16x = 24 - 3
x = 21 : 16
x= 1 ⁵/₁₆ или x = 1,3125