Доказательство: A и B - острые углы тупоугольного треугольника, значит угол С тупой и
0<A<90,0<B<90,90<C<180 и
cos C<0,cos A>0,cos B>0 (*)
tgA*tgB<1 равносильно неравенству
tgA*tgB-1<0
Рассмотрим левую часть неравенства, используя тригонометрические формулы
tg x=sin x\cos x
cos (A+B)= cosA*cosB- sinAsinB
cos(180-A)=-cos A
и соотношение углов треугольника A+B+C=180 и учитывая (*):
tgA*tgB-1=sinA\cos A*sin B\cos B-1=(sinAsinB-cosA*cosB)\(cos A*cos B)=
=-cos(A+B)\(cos A*cos B)=cos(180-(A+B))\(cos A*cos B)=cos C\(cos A*cos B)<0,
А значит tgA*tgB-1<0, или tgA*tgB<1, что и требовалось доказать.
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) в это же число раз.
Если величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры.
1. Пешеход за 1 ч проходит 4 км, за 2 ч - 8 км, за 3 ч - 12 км и т.д. Т.е. время увеличивается, следовательно, и пройденный путь увеличивается в то же число раз.
Можно сказать, что пройденное расстояние прямо пропорционально времени.
4 : 1 = 8 : 2 = 12 : 3 = ... = 4.
2. Батон в магазине стоит 2 р., за 2 батона заплатят 4 р., за 3 батона - 6 р., за 4 батона - 8 р. и т. д. Т. е. количество батонов увеличивается,а, следовательно, увеличивается и стоимость покупки в то же число раз.
Можно сказать, что стоимость покупки батонов прямо пропорциональна их количеству.
2 : 1 = 4 : 2 = 6 : 3 = 8 : 4 = ... = 2.
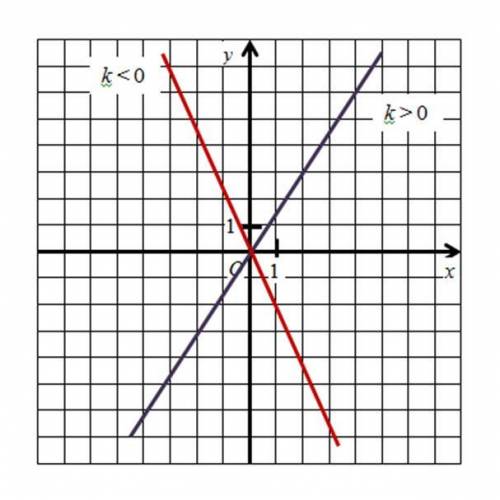
Т.о., прямую пропорциональность можно задать формулой у = kx, где k - коэффициент пропорциональности.
График - прямая, проходящая через начало координат.
Если k > 0, то график расположен в 1-й и 3-й координатных четвертях, если k < 0, то - во 2-й и 4-й (см. рис.)
Применяем разделительный (дистрибутивный) закон:
Перенесем 6 в левую часть выражения
Умножив 5 на 6, получим 30:
Умножив 6 на
Записываем
Разлагаем
Упростим, прибавляя члены.
Уберем ненужные скобки:
Вычтем
Упростим с прибавления чисел.
Складываем
Складываем
ответ: