64
Объяснение:
допустим число состоит из цифр а и b, 1≤a≤9, 0≤b≤9
само число можно записать как 10a+b
По условию (a-b)*(10a+b)=128.
видно, что a>b, поэтому можно сказать, что 1≤a≤9, 0≤b≤8 и a>b
решение 1
видно, что число 128 дожно быть разбиваемо на два сомножителя, один из них однозначный, второй - двузначный.
128=2*2*2*2*2*2*2
видно, что однозначный множитель может быть либо 2, либо 4, либо 8
тогда получаем пары (2;64), (4;32) и (8;16)
a)пара (2;64), то есть a=6, b=4. a-b=2 подходит (2*64=128)
б)пара (4;32), то есть a=3, b=2. a-b=1 не подходит (1*32≠128)
в)пара (8;16), то есть a=1, b=6. a<b не подходит
ответ 64
Решение 2
Просто раскрываем скобки в уравнении (a-b)*(10a+b)=128
10a²+ab-10ab-b²=128
10a²-9ab-b²-128=0
b²+9ab-(10a²-128)=0
Решаем квадратное уравнение относительно b
D=(9a)²+4(10a²-128)
Очевидно, что √D дожен быть натуральным числом
попробуем подобрать, всего у на 9 чисел от 1 до 9
а=1, D=81+4(10-128)=-391, не подходит
a=2, D=-28, не подходит
a=3, D=577, √D не целый, не подходит
и т.д.
мы обнаружим, что только при a=6 D=3844 и √D=62
b=(-9*6±62)/2=(-54±62)/2
Очевидно, что подходит только знак +
b=(-54+62)/2=4
число 64
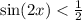
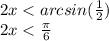
разделим обе стороны на 2 чтоб упростить
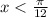
Функция синуса принимает положительные значения в первом и втором квадрантах. Для определения второго решения вычитаем решение из
π
, чтобы найти решение во втором квадранте.
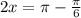
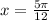
Период функции
sin(2х)
равен
π
, то есть значения будут повторяться через каждые
π
радиан в обоих направлениях
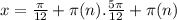
для всех целых n
Выбираем тестовое значение из каждого интервала и подставляем его в начальное неравенство, чтобы определить, какие интервалы удовлетворяют неравенству.
1.
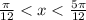
1 это ложно
2.
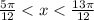
2 это истинно
3.
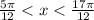
3 это ложно.
Итак
решение включает все истинные интервалы:
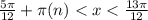
для всех целых n
(х + у) / 2 = 6
х + у = 12
Квадрат (12) = 144
144 - 70 = 74
Квадрат (х) + Квадрат (у) = 74
а дольше просто подобрала, но тебе придется применить формулу :)