я подозреваю что тут закралась неясность, в прогрессии насколько я помню количество элементов бесконечно, хотя в убывающей геометрической прогресии сумма всех элементов может сходиться.
инфми словами условие следует понимать так что n первых членов прогресии, где n = 2k,
выполняется условие 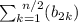 в три раза больше, чем
в три раза больше, чем 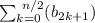
рассмотрим это более подробно на примере первых шести элементов
сумма нечетных S(1,3,5) = b1 + b3 + b5
сумма четных S(2,4,6) = b2 + b4 + b6 = b1*q + b3*q + b5*q = q(b1 + b3 + b5) = q*S(1,3,5)
следовательно отношение между четной суммой и нечетной равно знаменателю прогрессии.
Для нашей задачи это число 3
ответ 3
Если выкладываем 1 ряд то на первую клетку уйдет 4 палочки и 3 на каждую следующую
Каждый следующий ряд на первую клетку 3 палочки и по 2 на каждую следующую
Вариантов получить прямоугольник таким достаточно много
У Меня получились 402Х2, 286Х3, 86Х11, 79Х12, 56Х17 - можно дальше считать, мне кажется, что в условии не все данные
Для вычисления размеров надо по первому столбцу составить ряд 4,7,10,13,16 и т д
По второму 3,5,7,9,11 соответственно
Вычитаем из 2012 число из первого ряда и остаток делим на число из второго - должно делиться без остатка
А дальше посчитать периметр и учетверенную площадь легко
402Х2
P=804+4=808
S*4=804*4=3216
286X3
P=578
S*4=3432 и т.д.
1) 90°<143°<180° - Вторая четверть, sin143°>0 , cos143°<0 , tg143°<0 , ctg143°<0
2) -243° - вторая четверть. sin(-243°)>0 , cos(-243)°<0 , tg(-243°)<0 , ctg(-243°)<0
3) 735° . Весь круг - 360° , 360 * 2 =720° + ещё немного. Это значит, что 735° в 1 четверти. sin735°>0, cos735°>0 , tg735° и ctg 735° > 0.
4)-735°. -735° в 4 четверти. sin(-735°)<0 , cos(-735°)>0 + , tg(-735°) и ctg(-735°) < 0.
5) 300° - 3 четверть , sin(300°)<0 , cos(300°)<0 + , tg(300°) и ctg(300°) > 0 .
6)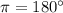 ,
, 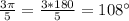 ∈ 2 четверти,
∈ 2 четверти, 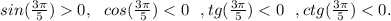
7)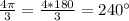 , ∈ 3 четверти ,
, ∈ 3 четверти , 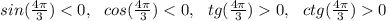
8) 1 радиан ≈ 57° . -0,5 радиан - 4 четверть. sin(-0,5)<0 , cos(-0,5)>0 , tg(-0,5) < 0 ,ctg (-0,5) <0
9) 4 радиана ∈ 3 четверти (4*57°≈228° ), sin4<0 , cos4<0 , tg4>0 , ctg4>0
10) -7,3 ∈ 4 четверти (-7,3*57°≈-416,1°), sin(-7,3) <0 , cos(-7,3) >0 , tg(-7,3) <0 , ctg(-7,3) <0.