ответ: 43
Объяснение:
Пусть одно из чисел равно 
, тогда второе 
.
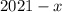Пусть:
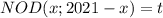
Тогда:
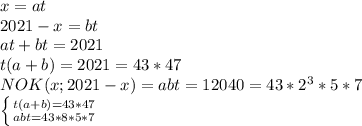
Где 
и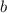 
взаимнопростые натуральные числа. Для определенности будем считать, что 
.
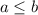Заметим, что числа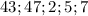 
простые. Из второго уравнения очевидно, что 
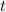не делится на 
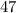, то есть 
.
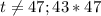Предположим теперь, что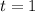 
, тогда 
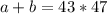, но тогда, поскольку сумма двух чисел делится на 
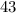, то либо каждое из них делится на 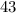, либо не одно из них не делится на 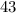. Если каждое из них делится на 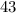, то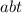 
делится на 
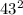, но правая часть второго равенства делится только на первую степень числа 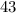. Если же оба из них не делятся на 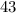, то с учетом того, что 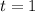, 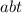не делится на . То есть мы пришли к противоречию.
Как видим, остается единственный вариант:
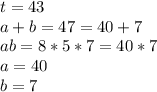
(6a+12b)+(2am+4bm)
m(6a+2a)+(12b+4b)
m(7a+16b)