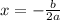
1) 
Область определения
{ 3x - 4 > 0; x > 4/3
{ 12 - 5x > 0; x < 12/5
D(x): x ∈ (4/3; 12/5)
Так как основания логарифмов одинаковые, то и выражения под логарифмами равны.
3x - 4 = 12 - 5x
3x + 5x = 12 + 4
8x = 16; x = 2 ∈ (4/3; 12/5) - это решение.
2) 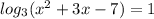
Область определения:
x^2 + 3x - 7 > 0
D = 3^2 - 4*1(-7) = 9 + 28 = 37
x1 = (-3 - √37)/2 ≈ -4,541; x2 = (-3 + √37)/2 ≈ 1,541
D(x) : x ∈ (-oo; (-3-√37)/2) U ((-3+√37)/2; +oo)
Логарифм - это показатель степени, в которую надо возвести основание, чтобы получить число под логарифмом.
x^2 + 3x - 7 = 3^1 = 3
x^2 + 3x - 10 = 0
(x + 5)(x - 2) = 0
x1 = -5 ∈ D(x); x2 = 2 ∈ D(x) - это два решения.
3) 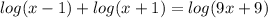
К сожалению, мы не знаем основание логарифма, но это неважно.
Главное, что основание должно быть везде одинаковое.
Область определения:
{ x > 1
{ x > -1
D(x) : x ∈ (1; +oo)
Решаем уравнение
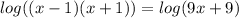
Так как основание везде одинаковое, можно перейти к выражениям
(x - 1)(x + 1) = 9x + 9 = 9(x + 1)
Так как x = -1 не может быть, то делим все на (x + 1)
x - 1 = 9
x = 10 - это решение.
7/Задание № 5:
В двух корзинах 79 яблок, причём 7/9 первой корзины составляют зелёные яблоки, а 9/17 второй корзины - красные яблоки. Сколько зелёных яблок в первой корзине?
РЕШЕНИЕ: Пусть в первой корзине а яблок. Это число а должно делиться на 9, так как 7/9 первой корзины составляют зелёные яблоки, а это натуральное число. Пусть во второй корзине b яблок, тогда по той же причине b должно быть кратно 17, так как 9/17 второй корзины - красные яблоки.
Тогда уравнение 9p+17q=79 даст такие натуральные p и q, что p - (1/9) часть яблок в первой корзине, q - (1/17) часть яблок во второй корзине.
9p+17q=79
17q=79-9p
p=1: 79-9=70, 70 не делится на 17
p=2: 79-18=61, 61 не делится на 17
p=3: 79-27=52, 52 не делится на 17
p=4: 79-36=43, 43 не делится на 17
p=5: 79-45=34, q=34/17=2
p=6: 79-54=25, 25 не делится на 17
p=7: 79-63=16, 16 не делится на 17 и результат менее наименьшего натурального числа 1, поэтому проверку можно завершить.
Значит, p=5 - (1/9) часть яблок в первой корзине, зеленых же яблок 7/9 от общего числа, то есть в 7 раз больше, чем величина р: 5*7=35.
ОТВЕТ: 35 яблок