Рассмотрим последние цифры степеней чисел 3 и 7 (очевидно, степени чисел 33 и 77 оканчиваются на те же цифры; в таблице последняя цифра числа x обозначена как x mod 10):
Дальше таблицу можно не продолжать: поскольку последняя цифра степени определяется только последней цифрой предыдущей степени, то дальше всё будет повторяться: например, для степеней тройки дальше идут 3, 9, 7, 1, 3, 9, ... Таким образом, последовательность последних цифр степеней тройки и семёрки является периодической с периодом 4, то есть прибавление любого количества четвёрок к показателю степени последнюю цифру не меняет.
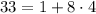, поэтому 
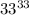оканчивается на ту же цифру, что и 
, то есть на 3. 
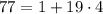, поэтому 
оканчивается на ту же цифру, что и 
, то есть на 7. Значит, сумма 
оканчивается на ту же цифру, что и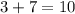 
, то есть на 0. Искомый остаток равен нулю.
ответ. 0
Со скобками нужно решать, смотря какие знаки стоят в примере + или --
Объяснение:
При сложении 2 многочленов, нужно представить их в стандартном виде, потом чтобы сложить их, нужно:
1) Раскрыть скобки, не меняя знаки, потому что при + не меняется знак на противоположный.
При -- нужно опустить скобки и заменить все знаки одночленов внутри скобок на противоположные, например: 3х2-5ху-7х2у+(5ху--3х2+8х2у) =3х2-5ху-7х2у+5ху-3х2+8х2у.
Без скобок решается по разложения многочленов на множители:
1. Вынесение общего множителя за скобки
10а+25b
группировки
сокращённого умножения.
Да и ты можешь посмотреть ролики в интернете, найми репетитора.
Sбок = 1/2* Росн* h ( где h - апофема - высота боковой грани)
Смотрим боковую грань - равнобедренный треугольник. провели апофему, получили прямоугольный треугольник, в котором гипотенуз = 5, катет= 3, второй катет = h = 4 (это египетский треугольник)
S бок = 1/2* 9* 4 = 18
S осн. = 1/2*3*3*√3/2 9√3
S = 18 + 9√3