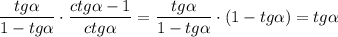
Объяснение:
Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k=tg α.
Угол наклона прямой равняется 0 только при параллельности ох и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0. Значит, вид уравнения будет y=b.
Если угол наклона прямой y=kx+b острый, тогда выполняются условия 0<α<
π
2
или 0°<α<90°. Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию tg α>0, причем имеется возрастание графика.
Если α=
π
2
, тогда расположение прямой перпендикулярно ох. Равенство задается при равенства x=c со значением с, являющимся действительным числом.
Если угол наклона прямой y=kx+b тупой, то соответствует условиям
π
2
<α<π или 90°<α<180°, значение углового коэффициента k принимает отрицательное значение, а график убывае