1. Розничная цена товара составляет 425*1,12=476 руб.
Можно решить в два действия.
а) найдем наценку. 425 :100*12=51 (руб.)
б)найдем розничную цену товара
425+51=476 руб.
2. решаем задачу выражением (249,4-215)/215=0,16, тогда
0,16=16%
или снова по действиям.
а) найдем наценку в рублях.249,4-215=34,4 (руб).
б) найдем, сколько % от 215 составляет 34,4
34,4*100/215=16
3) Снова решаем или выражением, или по действиям.
Выражением: 755,2 :1,18=640 (руб.)
По действиям:
а) Узнаем, сколько процентов приходится на 755,2
100%+18%=118 %
б) найдем 1% 755,2/118=6,4
в) найдем базовую стоимость товара.6,4*100=640 (руб.)
Выбирайте тот которым Вы обычно решаете эти задачи в классе.
Объяснение:
1) у = х² + х - 12
х²+х-12=0 (пересечение с осью Ох)
х1×х2=-12
х1+х2=-1
х1=-4; х2=3
f(0)=0²+0-12=-12 (пересечение с осью Оу)
ответ: Функция пересекает ось Ох в точках: (-4;0) и (3;0), и пересекает ось Оу в точке (0;-12).
2) у = -х² + 3x + 10=-(х²-3х-10)
х²-3х-10=0 (пересечение с осью Ох)
х1×х2=-10
х1+х2=3
х1=5; х2=-2
f(0)= -0²+3×0+10=10 (пересечение с осью Оу)
ответ: Функция пересекает ось Ох в точках:
(5;0) и (-2;0), и пересекает ось Оу в точке (0;10).
3) у = -8х² - 2x + 1
-8x²-2x+1=0 (пересечение с осью Ох)
D=b²-4ac=(-2)²-4×(-8)×1=4+32=36
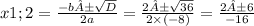
x1=-0,5; x2=0,25
f(0)=-8×0²-2×0+1=1 (Пересечение с осью Оу)
ответ: Функция пересекает ось Ох в точках:
(-05; 0) и (0,25; 0), и пересекает ось Оу в точке (0;1).
4) y = 7х² + 4х –11
7х²+4х-11=0 (Пересечение с осью Ох)
D=b²-4ac=4²-4×7×(-11)=16+308=324
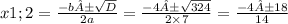
х1=1;
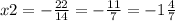
f(0)= 7×0²+4×0-11=-11 (пересечение с осью Оу)
ответ: Функция пересекает ось Ох в точках:
(1; 0) и (-1-(4/7); 0), и пересекает ось Оу в точке (0;-11).
y''+4y=0
Характеристическое уравнение:
k²+4=0
k²=-4
k=+-√(-4)=+-√4i²=+-2i
k=α+-β*i
α=0 β=2
Общее решение однородного ДУ имеет вид:
у.оо=exp(αx)*(C1*cos(βx)+C2*sin(βx))=
=exp(0)*(C1*cos(2x)+C2*sin(2x))=
=C1*cos(2x)+C2*sin(2x)
2) Найдем частное решение неоднородного уравнения
Правая часть имеет вид:
f(x)=3x*cos2x=exp(0*x)*((Ax+B)*cos2x+(Cx+D)*sin2x)
Т.к. k=α+βi=2i является корнем характеристического уравнения, тогда частное решение ищем в виде:
у.чн=x*((Ax+B)*cos2x+(Cx+D)*sin2x))=(Ax²+Bx)*cos2x+(Cx²+Dx)*sin2x
у.чн'=(A²x+Bx)'*cos2x+(Ax²+Bx)*(cos2x)'+(Cx²+Dx)'*sin2x+(Cx²+Dx)*(sin2x)'=
=(2Ax+B)*cos2x+(Ax²+Bx)*(-2)*sin2x+(2Cx+D)*sin2x+(Cx²+Dx)*2cos2x=
=(2Ax+B+2Cx²+2Dx)*cos2x+(-2Ax²-2Bx+2Cx+D)*sin2x
у.чн''=(2Ax+B+2Cx²+2Dx)' *cos2x+(2Ax+B+2Cx²+2Dx)*(cos2x)'+(-2Ax²-2Bx+2Cx+D)'*sin2x+(-2Ax²-2Bx+2Cx+D)*(sin2x)'=
=(2A+4Cx+2D)*cos2x+(2Ax+B+2Cx²+2Dx)*(-2)*sin2x+(-4Ax-2B+2C)*sin2x+(-2Ax²-2Bx+2Cx+D)*2cos2x=
=(2A+4Cx+2D-4Ax²-4Bx+4Cx+2D)*cos2x+
+(-4Ax-2B-4Cx²-4Dx-4Ax-2B+2C)*sin2x=
=(2A+8Cx+4D-4Ax²-4Bx)*cos2x+(-8Ax-4B-4Cx²-4Dx+2C)*sin2x
Подставим в исходное уравнение:
(2A+8Cx+4D-4Ax²-4Bx)*cos2x+(-8Ax-4B-4Cx²-4Dx+2C)*sin2x+
+(4Ax²+4Bx)*cos2x+(4Cx²+4Dx)*sin2x=3x*cos2x
(2A+8Cx+4D)*cos2x+(-8Ax-4B+2C)*sin2x=3x*cos2x
х*cos2x: 8C=3 C=3/8
cos2x: 2A+4D=0 ⇒ A=-2D
x*sin2x: -8A=0 ⇒ A=0
sin2x: -4B+2C=0 ⇒ -2B+C=0 ⇒ B=1/2C=1/2*3/8=3/16
D=0
Тогда
у.чн=3/16x*cos2x+3/8x²*sin2x
3) Найдем общее решение неоднородного уравнения:
у.он=у.оо+у.чн=
=C1*cos(2x)+C2*sin(2x)+3/16x*cos2x+3/8x²*sin2x