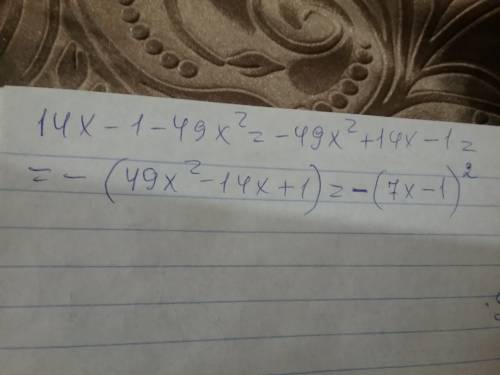
Пояснение:
Это квадратное уравнение можно решить сразу тремя : через теорему Виета и через Дискриминант (полный и краткий). Покажу все три.
(теорема Виета)
- можно применять, если первый (старший) коэффициент (а) равен единице (1), то есть квадратное уравнение имеет вид:
x² ± px ± q = 0.
x² + 8x + 15 = 0
p = 8; q = 15.
По т. Виета:
x₁ + x₂ = - 8,
x₁ × x₂ = 15.
x₁ = - 5,
x₂ = - 3.
<><><><><><><><><><><><><><><><>
IIа (Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
ax² ± bx ± c = 0.
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
D = b² - 4ac = 8² - 4 × 1 × 15 = 64 - 60 = 4 = 2².
D > 0 (значит, уравнение имеет два действ. корня)
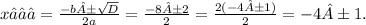
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
IIб ("краткий" Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
- можно применять к любым полным квадратным уравнениям вида:ax² ± bx ± c = 0,
где b - чётное число (то есть делится на 2 без остатка).
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
k = b ÷ 2 = 8 ÷ 2 = 4.
D₁ = k² - ac = 4² - 1 × 15 = 16 - 15 = 1.
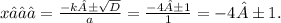
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
ответ: - 5; - 3.
Удачи Вам! :)
ответ
1) Не выполняя построения, определи, принадлежит ли графику функции y = x2 заданная точка A(1;−4).
Не принадлежит
2) Какая из указанных функций является линейной?
y = 14(x + 2)
3) Найдите область определения функции y = −8/5x.
D(y): x ≠ 0
4) ответ:
атмосферное давление на высоте 0,7 км равно 683,7 мм рт.ст.,
а на высоте 5 км равно 500,4 мм рт.ст.
Атмосферное давление равно 572,6 мм рт.ст. на высоте 4 км,
атмосферное давление равно 404,6 мм рт.ст. на высоте 10 км.
5) График функции y = 3x + 1 пересекает ось в точке с координатами:
(0 ; 1).
6) Дана функция y = −4 − t. При каких значениях t значение функции равно 7?
t = -11.
7) Заполни таблицу, если дана функция S(a) = a2.
Эта функция характеризует площадь квадрата (S), если известна сторона квадрата (a).
ответ: a — независимая переменная
Сторона a, см 3 5 7 9 11
Площадь S(a), см² 9 25 49 81 121
( Умнажайте на само число )
8) Функции заданы формулами f(x) = x2 + 1 и g(x) = x2 − 1. Сравни f(0) и g(10).
(В окошко ставь знак сравнения!)
ответ: f(0) < g(10).
Всё для вас ребята!
Удачи!