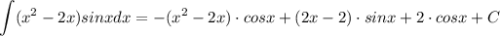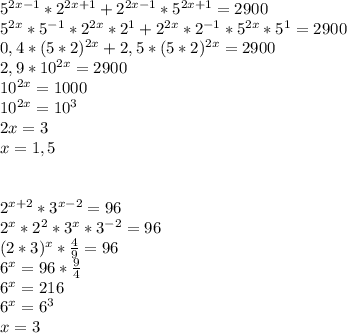
9x²- 4y² = 5.
(3х)²-(2у)²=5
(3х-2у) *(3х+2у) = 5
5 - число простое.
Произведение его множителей имеет 4 варианта из целых чисел:
5 = 1 · 5
5 = 5 · 1
5 = (-1) · (-5)
5 = (-5) · (-1)
Рассмотрим каждый из вариантов.
1 вариант.
(3х-2у) *(3х+2у) = 1*5
Получаем систему:
{3х-2у = 1
{3х+2у = 5
Сложим эти уравнения и получим:
3х-2у+3х+2у=1+5
6х = 6
х=1
Подставим х=1 во второе уравнение 3х+2у=5 и найдём у.
3*1+2у =5
2у=5-3
у=2 : 2
у=1
Получаем первую пару целых чисел:
х=1
у=1
2 вариант
(3х-2у) *(3х+2у) = 5*1
Получаем систему:
{3х-2у = 5
{3х+2у = 1
Сложим эти уравнения и получим:
6х=6
х=1
Подставим х=1 во второе уравнение 3х+2у=5 и найдём у.
3*1+2у=1
2у=1-3
2у = -2
Получаем вторую пару целых чисел:
х=1
у=-1
3 вариант
(3х-2у) *(3х+2у) = (-1) · (-5)
Получим систему:
{3х-2у = -1
{3х+2у = -5
Сложим эти уравнения и получим:
6х = -6
х=-1
Подставим х= -1 во второе уравнение 3х+2у=5 и найдём у.
3*(-1) +2у = -5
2у=-5+3
2у=-2
у=-1
Получаем третью пару целых чисел:
х = -1
у = -1
4 вариант
(3х-2у) *(3х+2у) = (-5) · (-1)
Получим систему:
{3х-2у = -5
{3х+2у = -1
Сложим эти уравнения и получим:
6х = -6
х=-1
Подставим х= -1 во второе уравнение 3х+2у=5 и найдём у.
3*(-1)+2у = -1
2у=3-1
у=1
Получаем четвёртую пару целых чисел:
х = -1
у = 1
ответ: (1; 1), (1; -1); (-1; -1); (-1; 1)
Есть формула 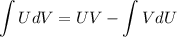
Но напрямую я её использовать не очень люблю.
Проще использовать такой подход (он, конечно, на формуле основан)
1. "Разрезать" функцию на 2 части: одну, которую будем дифференцировать, а другую - интегрировать. Понятно, что это разбиение часто основывается на том, какую функцию проще интегрировать, так как продифференцировать можно любую (но иногда, как во 2-м примере, будем смотреть, какую функцию лучше дифференцировать).
2. В столбик написать обе получившиеся функции (ту, которую интегрируем, с дифференциалом запишем, естественно). Отчертить большой чертой и справа напротив каждой функции написать результат того, что мы с ней делаем (в одном случае результат интегрирования, а в другом дифференцирования).
3. А дальше итоговый интеграл будет равен "функция на функцию" (это будет крест накрест, где нет дифференциалов) минус интеграл от произведения функций справа.
Попробую на примере показать:
а) есть интеграл 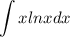
Здесь удобнее интегрировать логарифм, а дифференцировать 
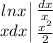
Ну вот как-то так. И теперь сам интеграл:
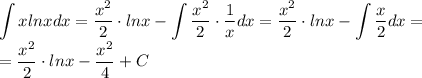
Надеюсь, что стало понятнее.
б) здесь придется интеграл по частям брать аж 2 раза, но ничего страшного, возьмем.
Сам интеграл 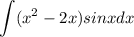
Здесь понятно, что тригонометрия будет давать тригонометрию что при интегрировании, что при дифференцировании, а вот многочлен уже при втором дифференцировании даст константу, так что его и будем дифференцировать.
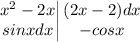
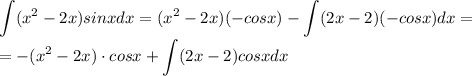
Надо лишь решить ещё один интеграл, причем абсолютно так же.
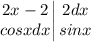
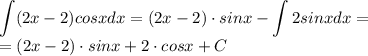
Ну и соберем все теперь: