Пусть х (км/ч) - скорость катера, тогда скорость катера по течению равна х+3 (км/ч), а против течения - х-3 (км/ч). Известно, что по течению катер проплыл 5 часов, в то время как против течения - 7 часов. Найдем пройденный путь для каждой ситуации:
S1 = (x+3)t1 - путь пройденный по течению, где t1 = 5ч
S2 = (x-3)t2 - путь пройденный против течения, где t2=7ч
Так как в обоих случаях пройден один и тот же путь, то S1 = S2. Приравняем их формулы и получим:
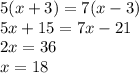
Таким образом, скорость катера в стоячей воде равна 18 км/ч.
По течению катер проплыл:
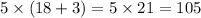
км
7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1) 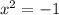
число в корне не может равняться отрицательному числу, корней уравнения нет.
2) 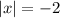
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1) 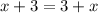
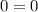
корней уравнения нет.
2) 
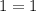
корней уравнения нет.
=> уравнения равносильные.
9. 1) 
ОДЗ: 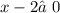 ,
, 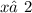 ;
;
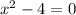
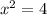
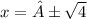
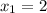 (не удовлетворяет ОДЗ),
(не удовлетворяет ОДЗ), 
ответ: 
2) 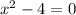
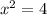
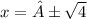
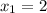 ,
, 
ответ:  ;
; 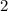
=> уравнения не равносильные.
10. 1) 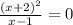
ОДЗ: 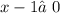 ,
, 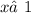 ;
;
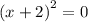
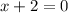

ответ: 
2) 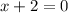

ответ: 
=> уравнения равносильные.

12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12. 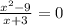
ОДЗ: 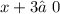 ,
,  ;
;
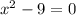


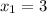 ,
,  (не удовлетворяет ОДЗ)
(не удовлетворяет ОДЗ)
ответ: 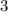
13. 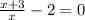
ОДЗ: 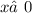 ;
;
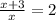
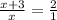
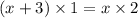
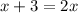
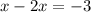
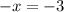
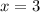
ответ: 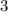
14. 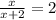
ОДЗ:  ,
,  ;
;
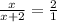
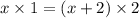

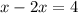


ответ: 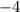
15. 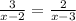
ОДЗ: 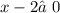 ,
, 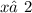 ,
, 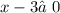 ,
,  ;
;
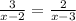
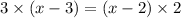
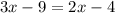
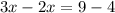
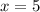
ответ: 
16. 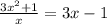
ОДЗ: 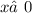 ;
;
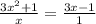
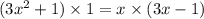
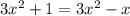
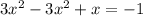

ответ: 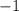
=(5z^2-6k+5z^2+3k)(5z^2-6k-5z^2-3k)+90z^2k=
=(10z^2-3k)(-9k)+90z^2k=
=-90z^2k+27k^2+90z^2k=27k^2