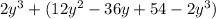
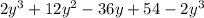
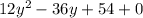
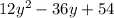
В решении.
Объяснение:
Решите задачу с составления уравнения. Разность двух чисел равна 17, а разность их квадратов 799. Найдите эти числа.
х - первое число.
у - второе число.
По условию задачи система уравнений:
х - у = 17
х² - у² = 799
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 17 + у
(17 + у)² - у² = 799
289 + 34у + у² - у² = 799
34у = 799 - 289
34у = 510
у = 510/34
у = 15 - второе число.
х = 17 + у
х = 17 + 15
х = 32 - первое число.
Проверка:
32 - 15 = 17, верно.
32² - 15² = 1024 - 225 = 799, верно.
Если изобразить эти сосны на графике - четырехугольник: сторона 14м перпендикулярна основанию (24м - расстояние между соснами), и вторая сторона 7м тоже перпендикулярна онованию.
Опускаем высоту из точки-макушки сосны 7 метров на первую сторону четырехугольника, она равна 24м (2 параллельные прямые, углы равны).
Теперь наш четырехугольник выглядит следующим образом: в основании прямогульный четырехугольник со сторонами 7м и 24м. А на нем лежит прямоугольный треугольник с катетами 24м и (14-7)м (т.е. 7м). Гипотенуза этого треугольника - искомое расстояние между макушками. Квадрат гипотенузы равен сумме квадратов катетов = 7^2+24^2 = 625
Гипотенуза = 25м