Область определения функции. ОДЗ: -00<x<+00
Точка пересечения графика функции с осью координат Y:График пересекает ось Y, когда x равняется 0: подставляем x=0 в x^2+4*x+3.
Объяснение:
a)
x²=xy+3
xy=-2 подставим это в первое уравнение
x²=-2+3=1
x₁=1 y₁=-2/x=-2
x₂=-1 y₂=-2/(-1)=2
b)
x(y+1)=0
x+5xy+y=4
1й случай х=0 подставим во второе уравнение получим у=4
2й случай у+1=0 у=-1 подставим во второе уравнение получим
х-5х-1=4 ; -4x=5 x=-5/4=0,8
c) этот пример не видно
другой номер
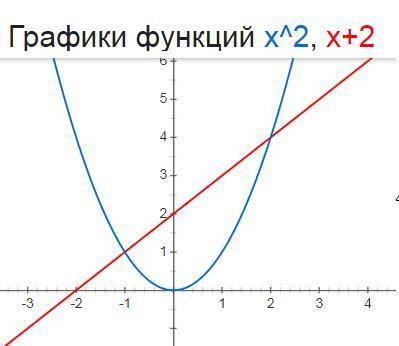
a) y=x^2 это парабола с вершиной в точке (0;0)
y=x+2 это прямая у=х которая является биссектрисой первой координатной четверти перемещенная вверх на 2 единицы
построим схематично графики
видно что графики имеют две точки пересечения значит система имеет два решения
если решать этот пример через дискриминант то тогда
x²=x+2
x²-x-2=0
d=1+8=9
x₁₋₂=(1±3)/2={-1;2}
1) а^3;
2) b^8;
3) представить в виде степени нельзя;
4) (0,5)^7;
5) х^4;
6) р^10;
7) q^9;
8) 7^8.
Объяснение:
1)a^5 : a^2 = а^(5-2) = а^3;
2)b^20 : b^12 = b^(20-12) = b^8.
3)-c^15:c^5 = - c^10 - это не степень, представить в виде степени нельзя;
4)(0,5)^17: (0,5)^10 = (0,5)^(17-10) = (0,5)^7;
5)x^11 : x^7 = х ^(11-7) = х^4;
6)p^19 : p^9 = р^(19-9) = р^10;
7)q^12 : q^3 = q^(12-3) = q^9;
8)7^20 : 7^12 = 7^(20-12) = 7^8.
Примечание:
Если в условии задания 3) минус вписан ошибочно, то решение такое:
3)c^15 : c^5 = с^(15-5) = c^10.