Відповідь:
Пояснення:
Якщо цифри в числі можуть повторюватися, то:
на перше місце числа можна поставити будь-яку цифру з трьох: 2, 3, або вибору;
вибір другої і третьої цифр можна здійснити 4-ма (можна вибрати кожну із даних цифр 0, 2, 3, або 5).
Тоді (за правилом добутку) можна утворити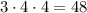 
трицифрових чисел.
Якщо цифри в числі не можуть повторюватися, то
на перше місце числа можна поставити будь-яку цифру з трьох: 2, 3, або вибору;
вибір другої цифри можна здійснити теж 3-ма (тут можна поставити і 0);
вибір третьої цифри можна здійснити вже 2-ма .
Тоді (за правилом добутку) можна утворити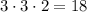 
трицифрових чисел.
а) х²=у≥0, тогда у²-8у+7=0, по Виету у=1; у=7, Вернемся к х,
х²=7⇒х=±√7; х²=1⇒х=±1
ответ х=±√7; х=±1
б) (х²-5х+4)(х²-5х+1)=28; х²-5х+1=у, тогда ( у+3)*у=28; у²+3у-28=0; по Виету у=-7; у=4, возвратимся к х, получим х²-5х+1=-7; х²-5х+8=0, дискриминант равен 25-32=-7- корней нет. х²-5х+1=4; х²-5х-3=0;х=(5±√(25+12)/2=
(5±√37)/2
ответ (5±√37)/2
в) о.з.=х*(х+1)*(х-1)≠0, ⇒х≠0; х≠±1;
(3х-5)*х+(6х-5)*(х+1)=(3х+2)*(х-1);
3х²-5х+6х²+6х-5х-5=3х²-3х+2х-2;
6х²-3х-3=0; 2х²-х-1=0; по Виету х=-1/2; х=1- не входит в ОДЗ уравнения.
ответ х=-1/2
x^2 + xy = - 2
x = 10 - 4y
( 10 - 4y )^2 + y( 10 - 4y ) + 2 = 0
100 - 80y + 16y^2 + 10y - 4y^2 + 2 = 0
12y^2 - 70y + 102 = 0
2( 6y^2 - 35y + 51 ) = 0
D = 1225 - 1224 = 1
y1 = ( 35 + 1 ) : 12 = 3
y2 = ( 35 - 1 ) : 12 = 17/6 = 2 5/6
x1 = 10 - 4 * 3 = - 2
x2 = 10 - 4 * ( 17/6 ) = 10 - (34/3 ) = 10 - 11 1/3 = - 1 1/3
ответ ( - 2 ; 3 ) ; ( - 1 1\3 ; 2 5\6 )