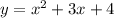
Найдем уравнение касательной, проходящей через точку с абсциссой 
Для этого найдем производную данной функции:

Найдем значение функции в точке с абсциссой  :
:

Найдем значение производной данной функции в точке с абсциссой  :
:
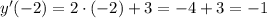
Уравнение касательной имеет вид:
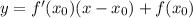
Подставим значение 

Итак, уравнение касательной заданной функции: 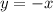
Воспользуемся геометрическим смыслом касательной: коэффициент наклона  касательной
касательной 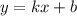 численно равен тангенсу угла наклона
численно равен тангенсу угла наклона 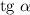 с положительным направлением оси
с положительным направлением оси 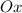
В найденной касательной коэффициент 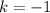 , следовательно,
, следовательно, 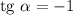 при
при  или
или 
ответ:  или
или 
m = p1^d1 * p2^d2 * p3^d3 * ... * pk^dk
n = p1^q1 * p2^q2 * p3^q3 * ... * pk^qk
Степени могут быть нулеывми.
Где p - простое. Рядом стоящая цифра - индекс.
^ - степень.
m + n = min(p1^d1, p1^q1) * min(p2^d2, p2^q2) * ... * min(pk^dk,pk^qk) + max(p1^d1,p1^q1)* ... * max(pk^dk, pk^qk)
С другой сторноы
m+n = p1^d1*p2^d2+p3^d3*...*pk^dk+p1^q1*p2^q2*...*pk^qk
Чтоб торжество было верно d1 > q1, d2 > q2, d3>q3, ... , dk > qk;
или наоборот d1 < q1, d2 < q2, d3 < q3, ... , dk < qk. Конец решения.
7•47=329
329+720=1049
ответ: 1049 руб