 - время, за которое разгружает машину первый грузчик, мин;
- время, за которое разгружает машину первый грузчик, мин; - время, за которое разгружает машину второй грузчик, мин;
- время, за которое разгружает машину второй грузчик, мин;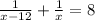 - время, за которое разгружают машину оба грузчика, мин;
- время, за которое разгружают машину оба грузчика, мин;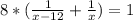
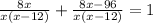
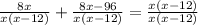
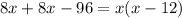
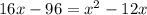
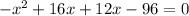
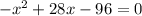

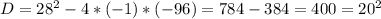
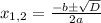
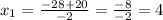
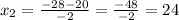
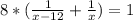
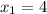 не подходит, так как время не может быть отрицательным. Следовательно ответ 24.
не подходит, так как время не может быть отрицательным. Следовательно ответ 24.
Подставим х=-32, у=-91:
-91=(-32)*3-5
-92 не= -101
ответ: точка К не принадлежит графику.