Объяснение:
Пусть длина равна х, а ширина - у. Тогда периметр прямоугольника равен 2*х+2*у, а площадь - х*у
Получаем систему:
2*х+2*у=26
х*у=42
2х+2у=26
2*(х+у)=26 (Делим обе части на 2)
х+у=13
Тогда х=13-у, представим х в нижнее выражение:
(13-у)у=42
13*у-у^2=42 (Перенесем все в правую часть(
у^2-13*у+42=0
Дискриминант =169-168=1, Дискриминант >0, 2 корня
у1=(13+1)/2=7
у2=(13-1)/2=6
Подставим в уравнение х+у=13 получившиеся значения и найдём х1 и х2 соответственно
х1+у1=13
х1+7=13
х1=6
х2+у2=13
х2+6=13
х2=7
Стороны прямоугольника равны 6 и 7
Сумма многочленов равна 4x²y+5xy-x²+5x-2
Степень многочлена равна 3
Объяснение:
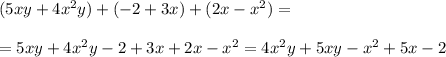
Данный многочлен является многочленом стандартного вида, т.к. это многочлен, каждый член которого является одночленом стандартного вида, а также, данный многочлен не содержит подобных членов.
Степенью многочлена стандартного вида называют наибольшую степень одночленов, образующих данный многочлен.
Степень первого одночлена (4x²y) равна 3 (2+1=3)
Степень второго одночлена (5xy) равна 2 (1+1=2)
Степень третьего одночлена (-x²) равна 2
Степень четвёртого одночлена (5x) равна 1
Степень пятого одночлена (-2) равна 0.
Итак, наибольшая степень равна 3, значит это многочлен третьей степени.
x≠0,x≠-1
40*(x+1)-36*x=2x(x+1)
2x²+2x-40x-40+36x=0
2x²-2x-40=0
x²-x-20=0
x1*x2=1 U x1*x2=-20
x1=-4 U x2=5