Уравнение прямой, отсекающей от первого координатного угла треугольник, имеет вид y=kx+b . Этот треугольник прямоугольный и его площадь равна половине произведения катетов.
Так как точка А(1;2) принадлежит этой прямой,то подставив координаты точки А(1;2) в это уравнение получим
Уравнение прямой теперь будет выглядеть так: 
.
Найдём точки пересечения этой прямой с осями координат:
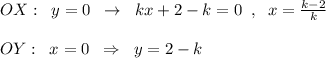
Длины отрезков, отсекаемых прямой y=kx+2-k на координатных осях, равны (2-k) на оси ОУ и (k-2)/k на оси ОХ. Эти отрезки и есть катеты прямоугольного треугольника. Вычислим его площадь:
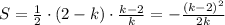
Найдём минимум это функции S(k).
Точка минимума: 
, так как при переходе через k= -2 производная меняет знак с минуса на плюс.
При k= -2 уравнение искомой прямой будет
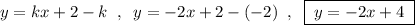
ответ: k= -2 .
Уравнение прямой, отсекающей от первого координатного угла треугольник, имеет вид y=kx+b . Этот треугольник прямоугольный и его площадь равна половине произведения катетов.
Так как точка А(1;2) принадлежит этой прямой,то подставив координаты точки А(1;2) в это уравнение получим
Уравнение прямой теперь будет выглядеть так: .
Найдём точки пересечения этой прямой с осями координат:
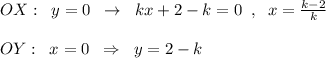
Длины отрезков, отсекаемых прямой y=kx+2-k на координатных осях, равны (2-k) на оси ОУ и (k-2)/k на оси ОХ. Эти отрезки и есть катеты прямоугольного треугольника. Вычислим его площадь:
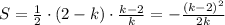
Найдём минимум это функции S(k).
Точка минимума: , так как при переходе через k= -2 производная меняет знак с минуса на плюс.
При k= -2 уравнение искомой прямой будет
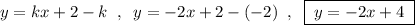
ответ: k= -2 .
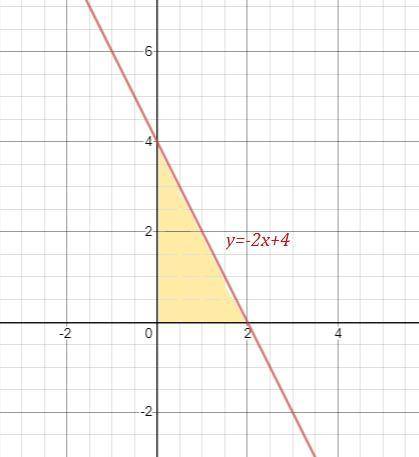
построить график функции y=|-x²+3x-2|
Заметим что y≥0 т.е. значения функции не могут быть отрицательными
теперь раскроем модуль
Для этого решим уравнение (найдем точки пересечения в осью Ох)
-x²+3x-2=0
-(x²-3x+2)=0
D=9-8=1
x₁=2; x₂=1
далее составим систему
Таким образом получаем график
см. в приложении