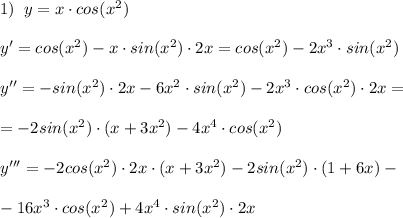
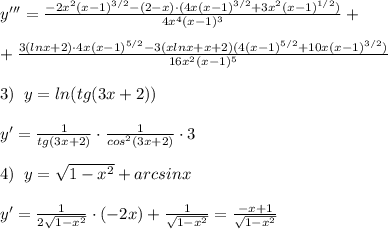
22
Объяснение:
1. Чтобы найти наибольшее значение функции, возьмем производную от этой функции и приравняем ее к нулю (т.к. минимумы и максимумы функции находятся в точках, где производная равна 0)
y' = 3x²-5x - 2 = 0
2. Решаем это квадратное уравнение:
D = 49
x_1 =( 5 -7 ) / 6 = -1/3 (не подходит, точка не принадлежит указанному промежутку).
x_2 = (5 + 7) / 6 = 2, принадлежит промежутку.
3. Находим значение функции в точке x = 2
y (x = 2) = 2³-2.5*2²-2*2+6 = 8 - 10 - 4 + 6 = 14 - 14 = 0
4. ВНИМАНИЕ: наибольшее значение может достигаться на краях промежутка , обязательно проверяем края
y (x = 0) = 0 - 2.5 * 0 - 2* 0 + 6 = 6
y (x = 4) = 4³ - 2.5 * 4² - 2*4 + 6 = 64 - 40 - 8 + 6 = 22
Итого, самое большое значение равно 22 и достигается в точке x = 4
Число под логарифмом должно быть строго положительно.
Если дробь равна 0, то числитель равен 0, а знаменатель не равен 0.
Область определения:
{ sin x > 0; x ∈ (2pi*k; pi+2pi*k)
{ cos x ≠ -√3/2; x ≠ 5pi/6 + 2pi*k; x ≠ 7pi/6 + 2pi*k
ОДЗ: x ∈ (2pi*k; 5pi/6 + 2pi*k) U (5pi/6 + 2pi*k; pi + 2pi*k)
Решаем уравнение
1)
sin x = 1
x1 = pi/2 + 2pi*k
2)
sin x = 1/2
x2 = pi/6 + 2pi*k
x3 = 5pi/6 + 2pi*k - не подходит
ответ: x1 = pi/2 + 2pi*k; x2 = pi/6 + 2pi*k
На промежутке [0; 3pi/2] будут корни x1 = pi/6; x2 = pi/2