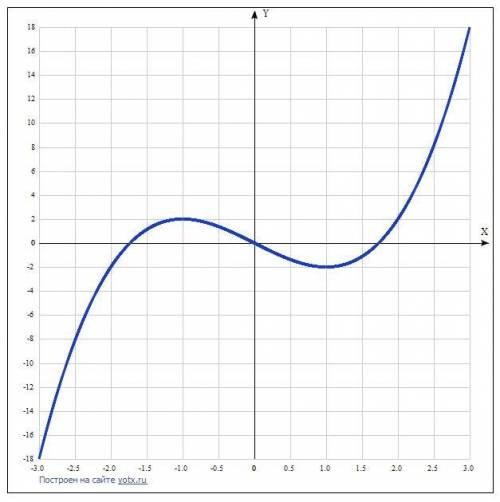
Таблица точек
x y
-3.0 -18
-2.5 -8.1
-2.0 -2
-1.5 1.1
-1.0 2
-0.5 1.4
0 0
0.5 -1.4
1.0 -2
1.5 -1.1
2.0 2
2.5 8.1
3.0 18
Точка пересечения графика функции с осью координат Y:
График пересекает ось Y, когда x равняется 0: подставляем x=0 в x³-3x.
у =0³-3*0 = 0,
Результат: y=0. Точка: (0; 0.
Точки пересечения графика функции с осью координат X:
График функции пересекает ось X при y=0, значит, нам надо решить уравнение:
x³-3x = 0
Решаем это уравнение и его корни будут точками пересечения с X:
x (х²-3) = 0,
х1 = 0, х2,3 = +-√3.
Результат: y=0. Точки: (0; -√3), (0; 0) и (0; √3).
Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y'=3x² – 3 = 0
Решаем это уравнение и его корни будут экстремумами:
3(х²-1) = 0,
х1 = 1, х2 = -1.
Результат: y’=0. Точки: (-1; 2) и (1; -2). Это критические точки.
Интервалы возрастания и убывания функции:
Найдем значения производной между критическими точками:
x = -2 -1 0 1 2
y' = 9 0 -3 0 9.
• Минимум функции в точке: х = -1,
• Максимум функции в точке: х = 1.
• Возрастает на промежутках: (-∞; -1) U (1; ∞)
• Убывает на промежутке: (-1; 1)
Точки перегибов графика функции:
Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции:
y'' = 6x = 0
Отсюда точка перегиба х = 0
Точка: (0; 0).
Интервалы выпуклости, вогнутости:
Находим знаки второй производной на промежутках (-∞; 1) и (1; +∞).
х = -1 0 1
y'' = -6 0 6.
Где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.
• Вогнутая на промежутках: (0; ∞),
• Выпуклая на промежутках: (-∞; 0)
Вертикальные асимптоты – нет.
Горизонтальные асимптоты графика функции:
Горизонтальную асимптоту найдем с предела данной функции при x->+oo и x->-oo. Соотвествующие пределы находим:
• lim x3-3x, x->+∞ = ∞, значит, горизонтальной асимптоты справа не существует
• lim x3-3x, x->-∞ = -∞, значит, горизонтальной асимптоты слева не существует
Наклонные асимптоты графика функции:
Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при x->+oo и x->-oo. Находим пределы:
• lim x3-3x/x, x->+oo = oo, значит, наклонной асимптоты справа не существует.
• lim x3-3x/x, x->-oo = oo, значит, наклонной асимптоты слева не существует.
Четность и нечетность функции:
Проверим функцию - четна или нечетна с соотношений f(-x)=f(x) и f(-x)=-f(x). Итак, проверяем:
• (-x3)-3(-x) = -x3+3x нет,
• (-x3)-3(-x) = -(x3-3x) – да, значит, функция является нечётной.
1
Объяснение:
Тк делители должны быть простыми числами(иначе не соблюдение условия про отсутствие однозначных делителей) Возьмем на пример 11 - рассматривается делитель простой и не однозначный,но даже его квадрат трехзначный-а у нас не может быть трехзначного делителя.
Почему я рассматриваю квадрат?Потому что мы доказываем ,что делитель только один.Поэтому я взяла в пример 11 тк это самое маленько число подходящие под наш критерий делителей.Дальше по логике могли бы быть только простые числа большие 11.Например,число дел на 11 и на 13 =>делится на 143.Значит,двучзначный делитель может быть только один.
(b-5)²=(b-5)(b-5)=b² -10b+25
(4a+c)²=(4a+c)(4a+c)=16a²+8ac+c²
(6x-y)(6x+y)=36x² - y²
(p²+q)(p²-q)=p^4 - q²
2.
x² - 81=(x-9)(x+9)
a²-6a+9=(a-3)(a-3)=(a-3)²
3.
(y+5)²-(y-5)(y+5)=y²+10y+25-y²+25=10y+50=10(y+5)
при у=-4,7
10*( -4,7+5)=10 * 0,3=3
4.
4(5a-b)(5a+b)=4(25a² - b²)=100a² - 4b²
(c^4 + d³)²=c^8 + 2c^4d³ + d^6
(x+6)²-(x-6)²=(x+6+x-6)(x+6 - x+6)=2x * 12=24x
5.
(3x-2)²-(3x-1)(3x+1)= -2x
9x² -12x+4 - 9x² + 1= -2x
-2x+12x=1
10x=1
x=0.1
25a² -81=0
(5a-9)(5a+9)=0
5a-9=0
5a=9
a=9:5
a1=1.8
5a+9=0
5a= -9
a2= - 1.8
a=±1.8