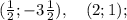
Объяснение:
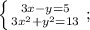
Выражаем из верхнего уравнения переменную "у":
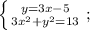
Подставляем полученное выражение в нижнее уравнение вместо "у":
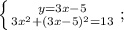
Раскрываем квадрат разности двух выражений, пользуясь следующей формулой:
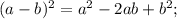
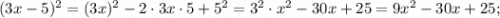
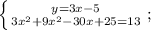
Приведём подобные слагаемые. Для этого вынесем общий множитель за скобки:
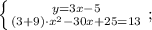
Выполним сложение в скобке и перенесём слагаемое 13 со знаком минус в левую часть уравнения:
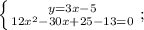
Выполним вычитание:
Разделив все части нижнего уравнения на 6, получим:
Теперь разделим все части нижнего уравнения на 2 для того, чтобы получить приведённое квадратное уравнение:
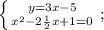
Решаем нижнее уравнение по теореме Виета. Согласно ей, сумма корней приведённого квадратного уравнения равна коэффициенту при "х", взятому с противоположным знаком, а их произведение — свободному члену:
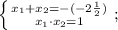
Минус перед скобкой и минус после скобки дают плюс:
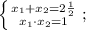
Корнями этой системы являются числа 1/2 и 2.
Мы нашли два значения переменной "х". Теперь подставим каждое из них в верхнее уравнение:
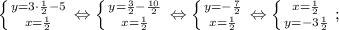
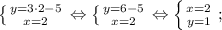
Мы получили две пары корней:
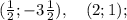
Они являются решениями системы.
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
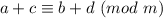
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
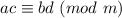
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
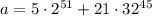
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,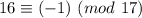 
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что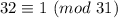 
, получаем
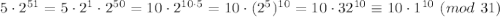
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
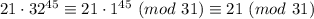
Остаток 21, чудесно. Выполняем последний шаг.
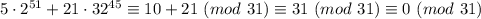
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
