t₁=200 (сек.)
t₂=600 (сек.)
Объяснение:
Первоначальная высота столба воды 5 метров, по условию задачи должна остаться четвёртая часть воды.
5:4=1,25 (м)
Подставляем все данные в формулу:
1,25=5-√2*10*5(это под корнем) * 1/400 *t + 10/2*(1/400)² * t²
1,25=5-√100 *t/400 + 5*1/160000 * t²
1,25=5-10*t/400 + 5t²/160000
1,25=5-t/40+t²/32000
Умножить уравнение на 32000, чтобы избавиться от дроби:
40000=160000-800t+t²
-t²+800t-160000+40000=0
-t²+800t-120000=0/-1
t²-800t+120000=0, квадратное уравнение, ищем корни:
D=b²-4ac =640000-480000=160000 √D= 400
t₁=(-b-√D)/2a
t₁=(800-400)/2
t₁=400/2
t₁=200 (сек.)
t₂=(-b+√D)/2a
t₂=(800+400)/2
t₂=1200/2
t₂=600 (сек.)
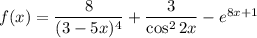
Совокупность всех первообразных функции 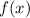 называют неопределенным интегралом:
называют неопределенным интегралом:
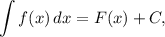
где 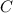 — произвольная постоянная.
— произвольная постоянная.
Тогда 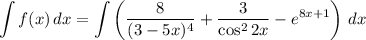
Теорема: если функции 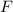 и
и 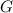 являются соответственно первообразными функций
являются соответственно первообразными функций 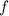 и
и 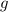 на промежутке
на промежутке 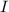 , то на этом промежутке функция
, то на этом промежутке функция 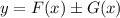 является первообразной функции
является первообразной функции 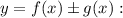
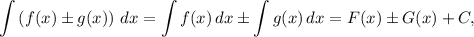
где 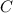 — произвольная постоянная.
— произвольная постоянная.
Тогда 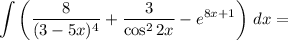
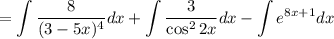
Теорема: если функция 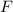 является первообразной для функции
является первообразной для функции 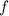 на промежутке
на промежутке 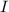 , а
, а 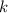 — некоторое число, то на этом промежутке функция
— некоторое число, то на этом промежутке функция 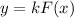 является первообразной функции
является первообразной функции 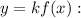
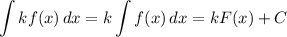
Тогда 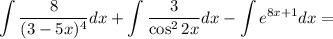
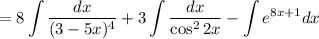
Теорема: если функция 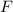 является первообразной для функции
является первообразной для функции 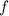 на промежутке
на промежутке 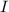 , а
, а 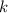 — некоторое число, отличное от нуля, то на соответствующем промежутке функция
— некоторое число, отличное от нуля, то на соответствующем промежутке функция 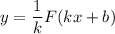 является первообразной функции
является первообразной функции 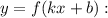
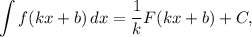
где 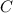 — произвольная постоянная.
— произвольная постоянная.
Найдем каждый интеграл по отдельности:
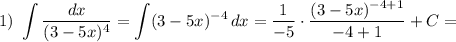
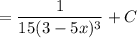
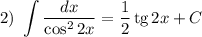
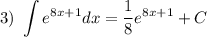
Получаем: 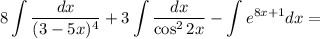
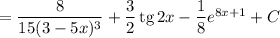
Таким образом, общий вид первообразных для функции 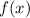 имеет вид:
имеет вид:
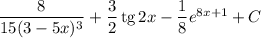
ответ: 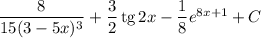
Использованные формулы интегрирования:
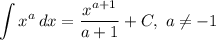
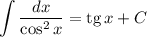
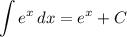
ответ: аn=1/(3n+4).