ответ:
y' = 4x^3-4x
приравниваем ее к нулю:
4x^3-4x = 0
x1 = 0
x2 = -1
x3 = 1
вычисляем значения функции
f(0) = 8
f(-1) = 7
f(1) = 7
fmin = 7, fmax = 8
используем достаточное условие экстремума функции одной переменной. найдем вторую производную:
y'' = 12x^2-4
вычисляем:
y''(0) = -4< 0 - значит точка x = 0 точка максимума функции.
y''(-1) = 8> 0 - значит точка x = -1 точка минимума функции.
y''(1) = 8> 0 - значит точка x = 1 точка минимума функции.
объяснение:
Правильно я условия записал?
1)
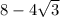= мы 4 выносим за скобки получится:
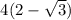= дальше мы 4 представляем как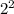 
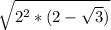= корень всё это время был и есть над этими числами просто ДО этого я типо его не писал, чтобы проще было смотреть. Теперь 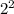это 4, корень из 4 = 2.
Вот и получается: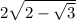 
2) 
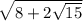использую формулу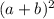 
получаем: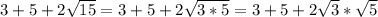 
дальше расставляем это так: 
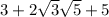и получаем формулу:
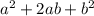сводим уравнение получается: 
.
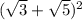Теперь не забываем, что у нас есть корень ещё один, который мы убрали, на время и получаем: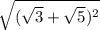 
, квадрат корней сокращается и получается: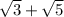 
f`(x)=3-4x
f`(1)=3-4=-1
f(1)=3-2=1
y=1+(-1)(x-1)=1-x+1=2-x