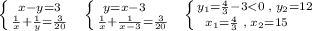Ввазе стоят 8 красных, 7 розовых и 5 белых гвоздик. сколькими можно выбрать пять гвоздик одинакового цвета

👇

Увидеть ответ

Ответ:

berezinaanna199

24.07.2022

Три если размышлять логично

4,5(52 оценок)

Открыть все ответы

Ответ:

kilutikkkasd

24.07.2022

1. Укажите линейное уравнение с двумя переменными.

1) 3·x-5=0 - только одна переменная х

2) х/7-у/5=8/3 - линейное, переменные х и у

3) 7/х+5/у=3/8 - нелинейное

4) 7·x²+5·у=3 - уравнение 2-степени

2. Укажите уравнение, решением которого является пара чисел (1 3/7; 2 5/6) .

Проверим подставкой в уравнение:

1) 14·x-12·y+14=0

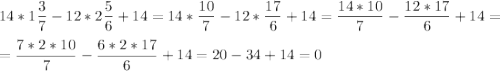
$\displaystyle 14*1\frac{3}{7} -12*2\frac{5}{6}+14=14*\frac{10}{7} -12*\frac{17}{6}+14=\frac{14*10}{7} -\frac{12*17}{6}+14=\\\\=\frac{7*2*10}{7} -\frac{6*2*17}{6}+14=20-34+14=0$

является решением, поэтому остальные уравнение не нужно проверить

2) 14·x-6·y-10=0

3) 10·x/7+17·y/6=27

4) x-6·y=17

3. Какая пара чисел является решением уравнения 3·x-2·y+5=0

1) (-1/3; -2) 2) (-2; -1/3) 3) (-4/3; -1/2) 4) (-3; 2)

Проверим подставкой в уравнение:

$1)\ \displaystyle 3*(-\frac{1}{3}) -2*(-2)+5=-\frac{3}{3} +4+5=-1+9=8\neq 0$

не является решением

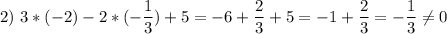
$2)\ \displaystyle 3*(-2) -2*(-\frac{1}{3})+5=-6+\frac{2}{3}+5=-1+\frac{2}{3}=-\frac{1}{3}\neq 0$

не является решением

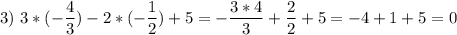
$3)\ \displaystyle 3*(-\frac{4}{3}) -2*(-\frac{1}{2})+5=-\frac{3*4}{3}+\frac{2}{2}+5=-4+1+5=0$

является решением, поэтому последнюю пару не нужно проверить

4. Какая из пар чисел является решением уравнением 2·x-y=6

1) (2; -1) 2) (5; 3) 3) (1; -4) 4) (-1; -3)

Проверим подставкой в уравнение:

1) 2·2-(-1)=4+1=5≠6 - не является решением

2) 2·5-3=10-3=7≠6 - не является решением

3) 2·1-(-4)=2+4=6=6 - является решением, поэтому последнюю пару не нужно проверить

4,5(93 оценок)

Ответ:

Kettiplay

24.07.2022

1 кран заполняет 1 бассейн за х часов, а второй кран за у=(х-3) часа.

Производительность 1 крана равна 1/х бассейна в час, а производительность 2 крана равна 1/(х-3) бассейна в час.

Совместная производительность двух кранов равна 1/х+1/(х-3) бассейна в час.

Вместе оба крана заполняют бассейн за 6 ч 40 мин=6 и 2/3 часа=20/3 часа.

Формула работы: A=p*t , где р - производительность, t - время. Объём работы принимаем за 1.

Тогда совместная производительность обоих кранов равна 1/(20/3)=3/20 бассейна в час .

Составим уравнение:

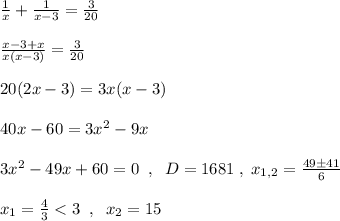
$\frac{1}{x}+\frac{1}{x-3}=\frac{3}{20}\\\\\frac{x-3+x}{x(x-3)}=\frac{3}{20}\\\\20(2x-3)=3x(x-3)\\\\40x-60=3x^2-9x\\\\3x^2-49x+60=0\; \; ,\; \; D=1681\; ,\; x_{1,2}=\frac{49\pm 41}{6}\\\\x_1=\frac{4}{3}$

Число, меньшее 3, не подходит, т.к. по условию x>3.

Бассейн заполняется 1 краном за 15 часов, а 2 краном за 15-3=12 часов.

$\left \{ {{x-y=3} \atop {\frac{1}{x}+\frac{1}{y}}=\frac{3}{20}} \right. \; \; \left \{ {{y=x-3\quad } \atop {\frac{1}{x}+\frac{1}{x-3}=\frac{3}{20}}} \right. \; \; \left \{ {{y_1=\frac{4}{3}-3$