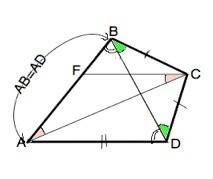
Проведем в данном четырехугольнике диагональ BD.
По услоию AF=FC, BC=CD, AB=AD ⇒
∆ АВD и ∆ ВСD - равнобедренные.
Рассмотрим треугольники АВС и АDС. Они равны по трем сторонам ( две по условию, сторона АС - общая)
Следовательно, ∠ВАС=∠DАС, ⇒ АС - биссектриса угла ВАD
В ∆ АFC стороны AF=CF, ∆ AFC – равнобедренный, ⇒ ∠FAC=∠FCA.
Но ∠ВАС=∠САD (из доказанного равенства ∆ АВС и ∆ АDС).
Из этого следует ∠FCA=∠CAD, а эти углы - накрестлежащие при пересечении FC и AD секущей АС.
Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти прямые параллельны. ⇒
FC||AD. Доказано.
Объяснение:
радиус равен корню из 16. 4 единицы. Центр х+2=0 и у+1=0
(-2;-1) На приложенном рисунке центр нарисован НЕПРАВИЛЬНО! он должен быть на 1 единицу НИЖЕ,
потом откладываете влево и вправо от центра по 4 единицы и получаете границы слев и справа. Из центра вверх и вниз по 4 единицы. И вы имеете 4 базовые точки рисуя плавные дуги подходящего рабиуса вы соединяете все 4 точки в окружностьМожете подставить в уравнение Х=0 получите из квадратного уравнения еще две точки на оси У. потом У=0 и получите еще точки на оси Х. останется только их аккуратно соединить.