Пояснение:
(!) Одно из свойств уравнений: любое число в уравнении можно перенести через знак равно (т. е. из левой части уравнения в правую, или из правой части в левую. При этом (обычно) переменные переносятся в левую часть уравнения, а числа - в правую) изменив знак перед числом на противоположный ("+" на "-" ; "-" на "+"). Такое уравнение будет равносильно исходному уравнению.
(!) При упрощении выражения и решения уравнения воспользуемся распределительным свойством умножении, относительно действия сложения и вычитания:
a × (b + c) = ab + ac.
a × (b - c) = ab - ac.
1) x (x - 8) - 20 = - 15 - x (1 - x);
x² - 8x - 20 = - 15 - x + x²;
x² - x² - 8x + x = - 15 + 20;
- 7x = 5;
x = 5 ÷ (- 7);
x = -  .
.
__________
ответ: -  .
.
2) 47 - x (11 - x) = 19x + x²;
47 - 11x + x² = 19x + x²;
x² - x² - 11x - 19x = - 47;
- 30x = - 47;
x = - 47 ÷ (- 30);
x = 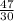 ;
;
x = 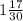
__________
ответ: 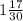 .
.
3) 33x - x² = (35 - x) x - 17;
33x - x² = 35x - x² - 17;
- x² + x² + 33x - 35x = - 17;
- 2x = - 17;
x = - 17 ÷ (- 2);
x = 8,5.
__________
ответ: 8,5.
4) 59x + 4x² = - 4x (1 - x) + 21
59x + 4x² = - 4x + 4x² + 21
4x² - 4x² + 59x + 4x = 21
63x = 21
x = 21 ÷ 63
x = 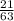
x = 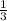 .
.
__________
ответ: 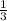 .
.
__________________
Удачи! :)
На первую позицию можно ставить одну из десяти букв, на вторую, одну из девяти и т.д. Получим: 10!
Найдём количество которыми можно составить слово математика из данного набора букв при учёте позиции той или иной буквы.
Е, И и К могут занимать только одну позицию, а вот А, М и Т можно менять местами.
Для М и Т это будет 2! и 2!, для А – 3!
С учётом порядка позиции их будет:
Тогда вероятность (согласно классическому определению):
Попробуем другой, более простой
Перестановки с повторением.
Всего у нас
Перестановка с повторением, которая даёт нам слово "Математика" всего одна, потому мы получаем вероятность: