1) Аналитический.
2) Рекуррентній.
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)

6)

7) Это арифметическая прогрессия. 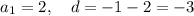
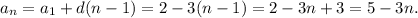
8)
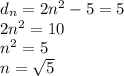
ответ: нет, не является, потому что 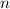 должно быть натуральным числом.
должно быть натуральным числом.
9) 
Наибольшее натуральное 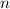 , удовлетворяющее этому неравенству, — это 16.
, удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
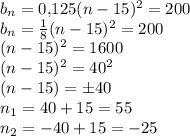
Второе решение не подходит, поскольку 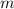 должно быть натуральным числом.
должно быть натуральным числом.
ответ: 
1) Аналитический.
2) Рекуррентній.
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)

6)

7) Это арифметическая прогрессия. 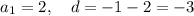
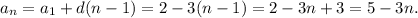
8)
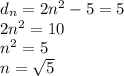
ответ: нет, не является, потому что 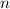 должно быть натуральным числом.
должно быть натуральным числом.
9) 
Наибольшее натуральное 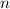 , удовлетворяющее этому неравенству, — это 16.
, удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
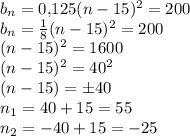
Второе решение не подходит, поскольку 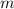 должно быть натуральным числом.
должно быть натуральным числом.
ответ: 
а₁₃ + а₁₆ = 4
Найти S₂₈
Решение.
1)
Выразим а₁₃ и а₁₆ через первый член прогрессии а₁ и знаменатель d.
a₁₃ = a₁ + 12d
a₁₆ = a₁ + 15d
В данное уравнение а₁₃ + а₁₆ = 4 подставим вместо а₁₃ и а₁₆ их значения.
а₁ + 12d + а₁ + 15d = 4
2a₁ + 27d = 4
2) А теперь к сумме S₂₈ применим формулу суммы первых n членов арифметической прогрессии
S₂₈ = (a₁ + a₁ + 27d)·14
S₂₈ = (2a₁ + 27d)·14
В скобках получилось выражение, которое равно 4 по результату из первого действия.
Заменим и получим.
S₂₈ = 4 · 14
S₂₈ = 56
ответ: S₂₈ = 56