Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются.
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
( abc… ) n = a n · b n · c n …
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
( a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
( a m ) n = a m n .
Здравствуй!
У тебя есть четкая граница: один график рисуешь, если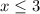 
, другой - при 
.
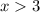Для удобства можно провести пунктирную вертикальную линию, пересекающую координату 3 на горизонтальной оси Ох (или, если быть точным, построить график функции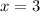 
). Это будет линией, разделяющих два графика.
Тогда ты строишь первый график, то есть 
, на левой части от этой границы, ведь именно левее у нас иксы меньше 3, а второй график,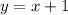 
, справа от неё.
Обычно в подобных заданиях графики сходятся в одной точке на границе и получается красивая картинка. Однако так происходит не всегда.
В твоём же случае графики не сходятся в одной точке (кстати ты правильно начал строить, к ответу я прикрепил скриншот того, как должно получиться), а потому ты внимательно смотришь, к какому из графиков точка 3 принадлежит, а к какому - нет.
В данном случае точка с абсциссой 3 (т.е. с иксовой координатой) принадлежит первому графику, на "границе" закрась эту точку, это будет означать то, что здесь график прерывается
А вот второму графику точка с абсциссой 3 не принадлежит; тебе нужно на "границе" "выколоть" эту точку - то есть обозначить не закрашенным кружком, а пустым кружком.
Успехов!
