Подробное объяснение: в задании номер 1 число 3 в 4 степени возводится в 5 степень. Когда ты видишь что-то наподобие этого, то степени перемножаются: то есть 4 степень умножаем на 5 степень и получаем 20 степень, то есть 3 в 20 степени. Далее, в числителе, видим:
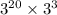
Здесь степени тоже умножаюся, потому что умножаются сами числа. Перемножаем и получаем 3 в 23 степени. Ну и затем остается сократить то, что получилось:
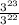
Сокращаем и получаем:
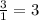
Задание номер 2.
Ну, тут все просто, тут надо правильно перемножить, как на фото. С умножением степеней ситуация та же, что и в 1 задании.
Надеюсь
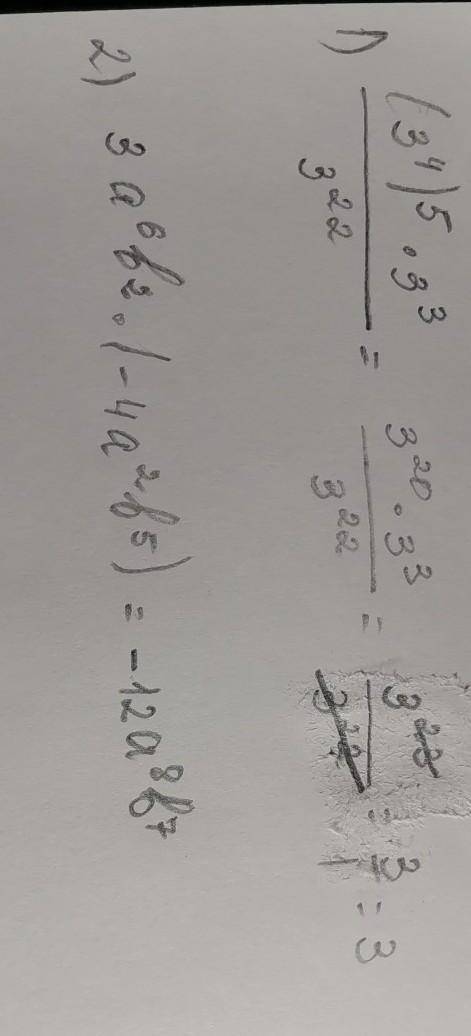
-3.
Объяснение:
√(6 -2√5) - √(9+4√5) =
Заметтм, что каждое подкоренное выражение можно представить в виде квадрата суммы или разности:
6 -2√5 = 5 -2√5 + 1 = (√5)^2 -2•√5•1 + 1^2 =
(√5 -1)^2.
9 + 4√5 = 5 + 4√5 + 4 = (√5)^2 + 2•√5•2 + 2^2 =
(√5 + 2)^2.
Именно поэтому решение запишется так:
√(6 -2√5) - √(9+4√5) = √(√5 -1)^2 - √(√5 + 2)^2 = l√5 - 1l - l√5 + 2l
Выражения, записанные под знаком модуля положительные, знак модуля опускаем, не меняя знаки слагаемых в скобках:
(√5 - 1) - (√5 + 2) =
Упрощаем получившееся выражение:
√5 - 1 - √5 - 2 = -1 -2 = -3.
ответ: -3.
Использованные тождества:
а^2 - 2аb + b^2 = (a-b)^2;
а^2 + 2аb + b^2 = (a+b)^2;
√(a)^2 = lal.
x ≠ -3